Metastabilty
Ryan Robucci
• ESC/O-Key to see slide overview • ? to see help
References
- ꭝ High Speed Digital Design: A Handbook of Black Magic 1st Edition by Howard Johnson (Author), Martin Graham (Author)
Digital Abstraction and Noise
- consider a chain of digital gates
- signal corruption model: ideal gates with noise sources
- desire proper interpretation of binary values in presence of noise
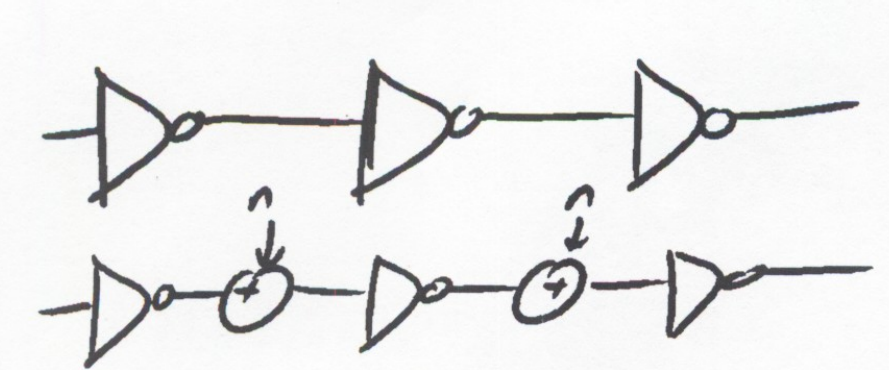
Sources of Noise:
- Electronic Thermal Noise
- Power/Ground Current (through supply resistance)
- Fast Signals in the System (large dI/dt induces drops in supply inductance)
- Signal Coupling: Mutual Cap. and Mutual Inductive
- Ringing (draw if required)
- Temperature Differences between components affecting threshold voltages
(3-6 are esp. important for fast systems)
Additionally, manufacturing between devices can introduced fixed noise (e.g. offsets)
Noise Margins
- Noise margins ensure correct digital operation, maintaining the digital abstraction
- Require voltage constraints on inputs, and outputs to satisfiy input constraints for the downstream gate even in the presence of noise
- The difference between the output and input constraint are known as the Noise Margins
- Noise Margin High is the margin for
'1' - Noise Margin Low is the margin for
'0'
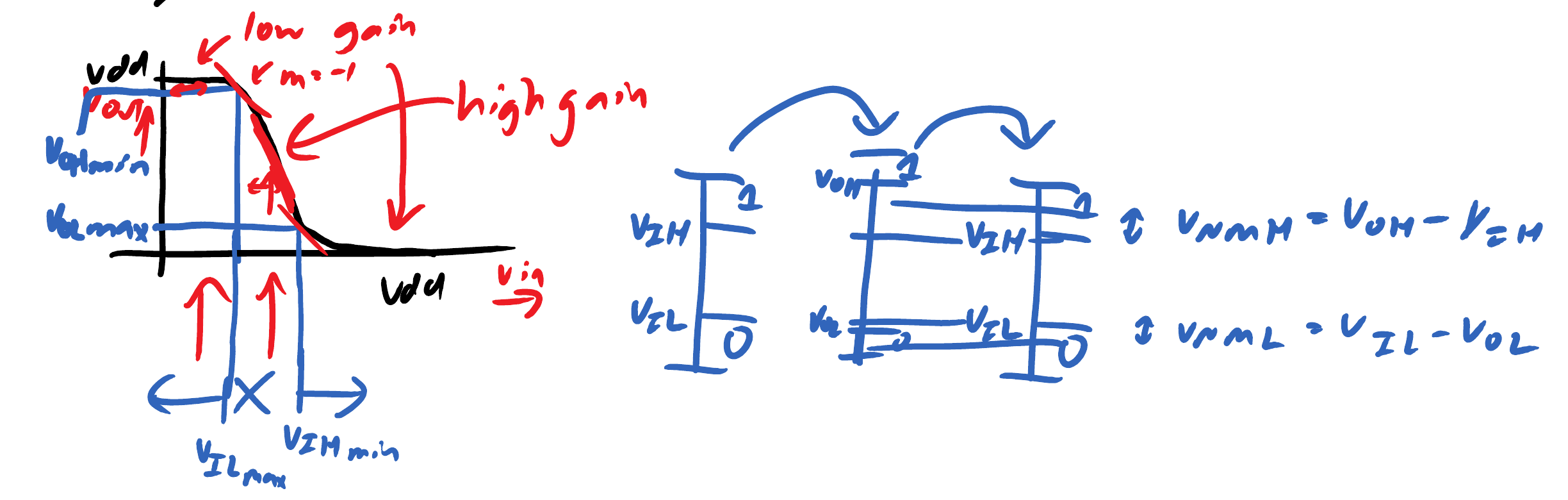
Noise F.O.M.
- Some corruption is proportional to voltage swings
- Examples:
- larger transition -> larger ringing
- larger transition -> larger disturbance on neighboring signal lines
- Examples:
- Noise Performance Figure of Merit: Ratio of Noise Margin to Voltage Swing is a useful figure of merit (FOM)
For example: for two logic families, noise margins that are proportional to the power supply level may perform roughly the same
FOM=Voltage SwingNoise Margin=VOH−VOLVOH−VIH or VOH−VOLVIL−VOL
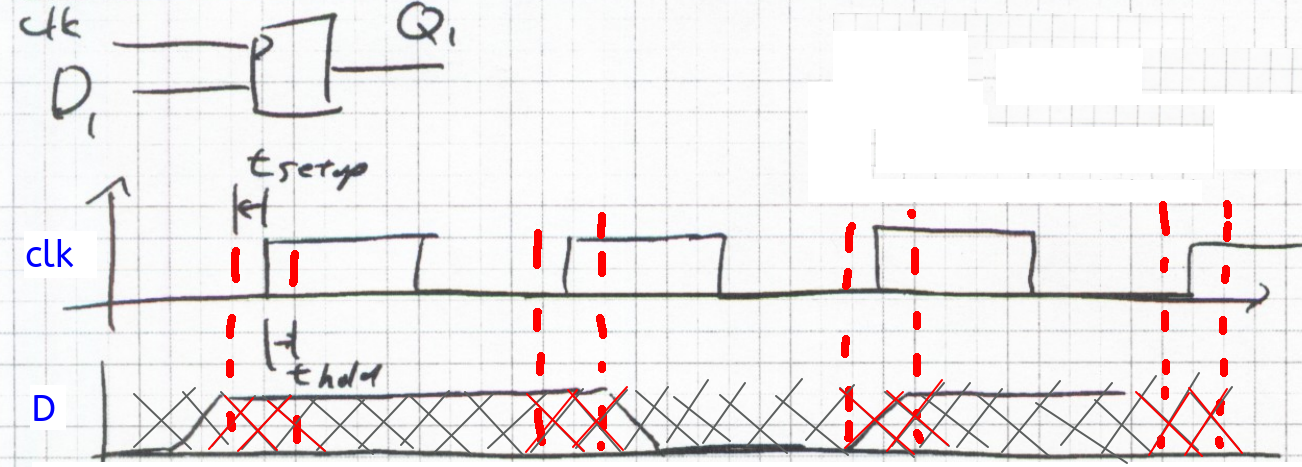
Timing Requirements for Registers
- Registers tend to have voltage as well as specific timing requirements for the inputs
- Setup and Hold
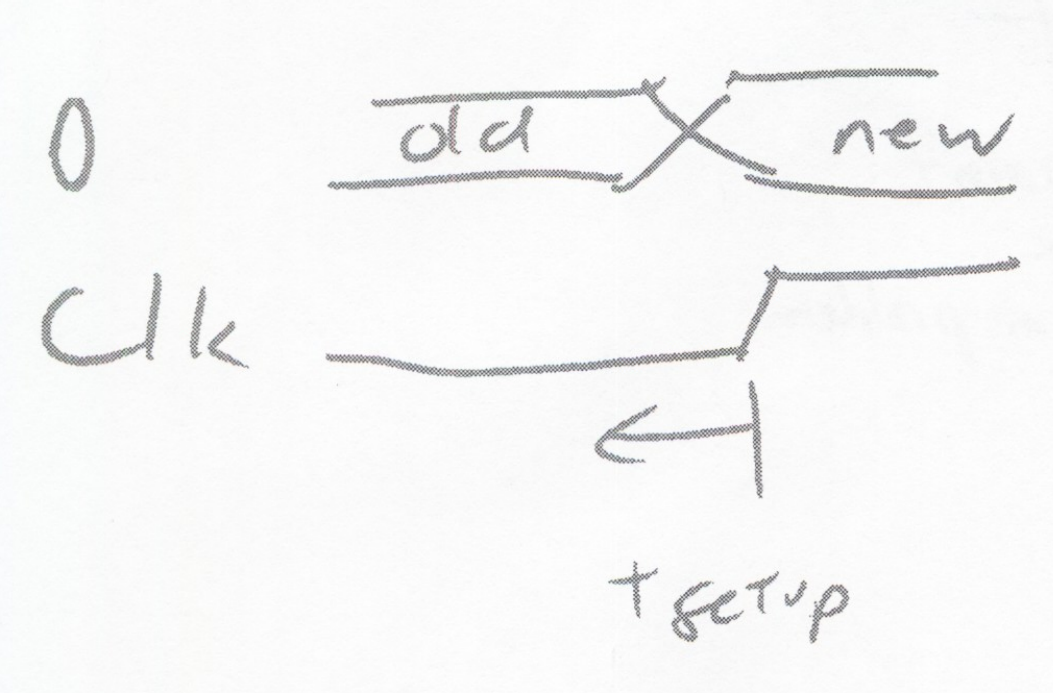
- If violated, may get
- Old Data
- New Data
- Metastable Output
- Not conform to voltage specifications
- May change in middle of clock period (multiple output transitions triggered by the clk)
Possible Output transitions when expected is 0->1:
Clock Domain Crossing
- Clock Domain Crossing arises from the need to communication between Multiple Clock Domains
- You have learned in sync. design in one clock domain
- Having Multiple Clock Domains means Clock Domain Crossing must be considered
Async Inputs
Not all signals arise from a clock domain at all, such as physical, real-world inputs
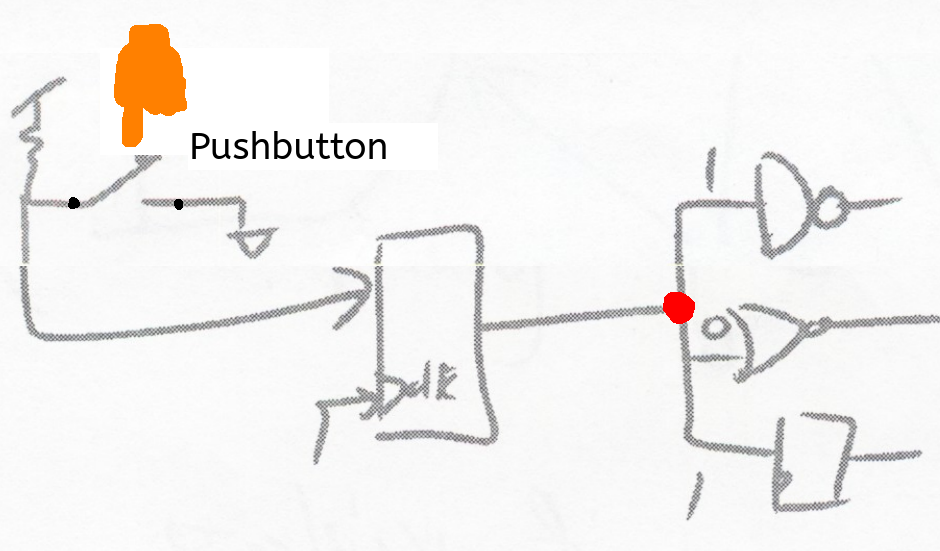
A problem arises at a fanout point, where mutiple interpretations are performed in parallel
Metastabilty
Consider that an inverter represents contrain on allowed input, output (V1,V2) relationships:
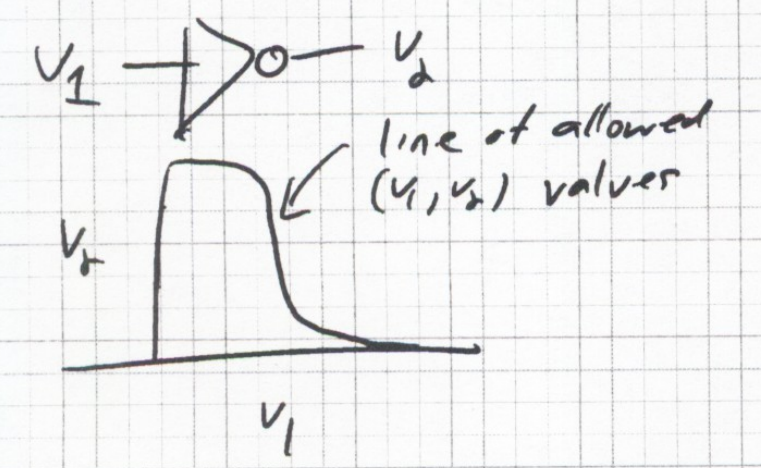
Consider another inverter with the input and output connections reversed:
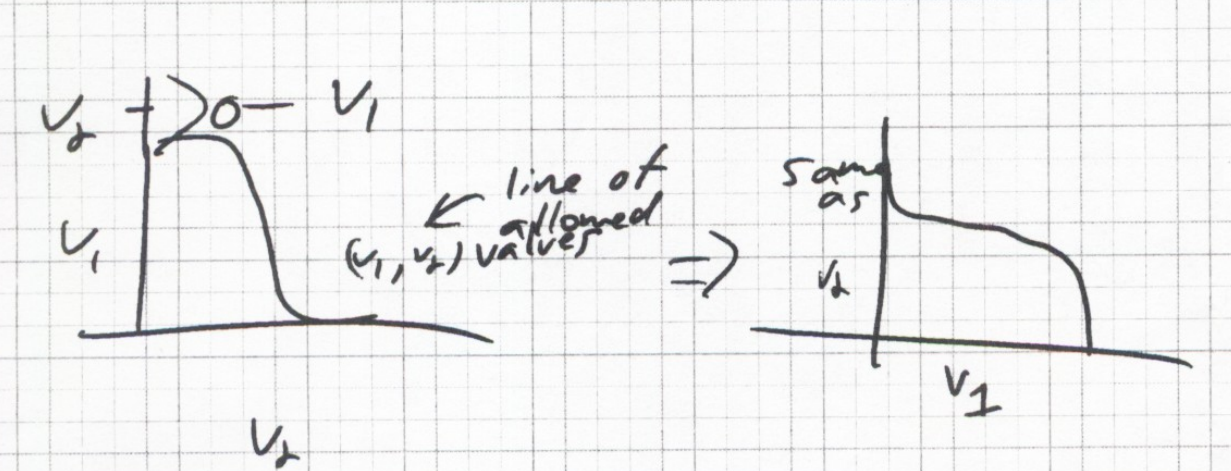
Consider a coupled set of inverters, setting constraints between V1 and V2
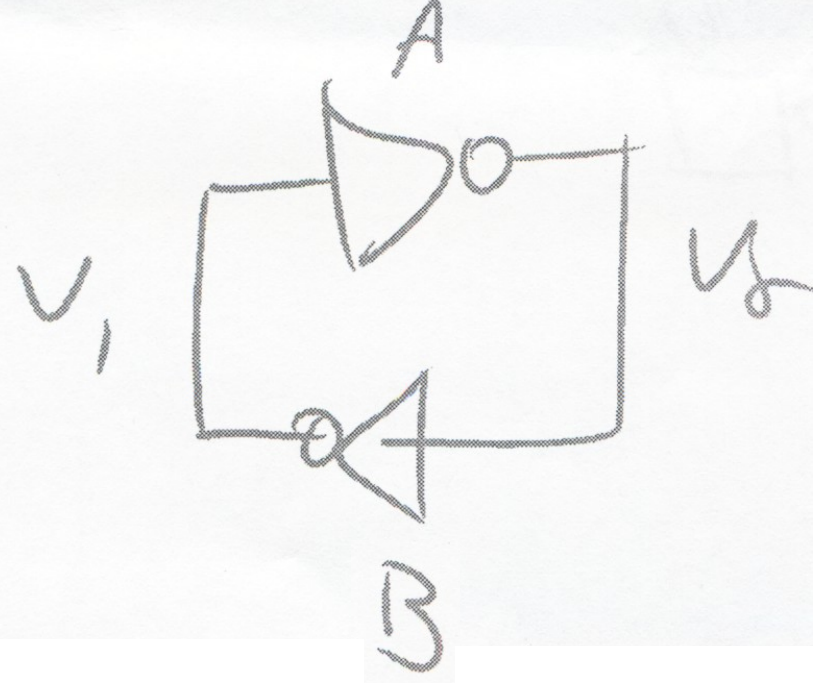
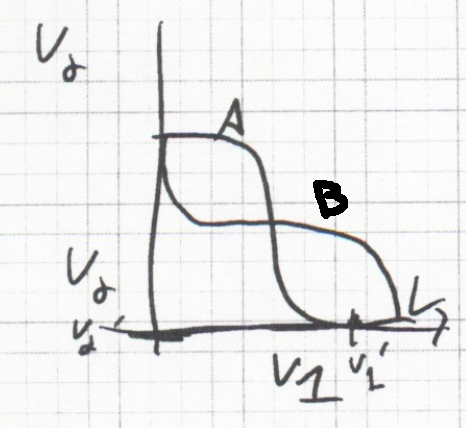
Two constraints, A and B
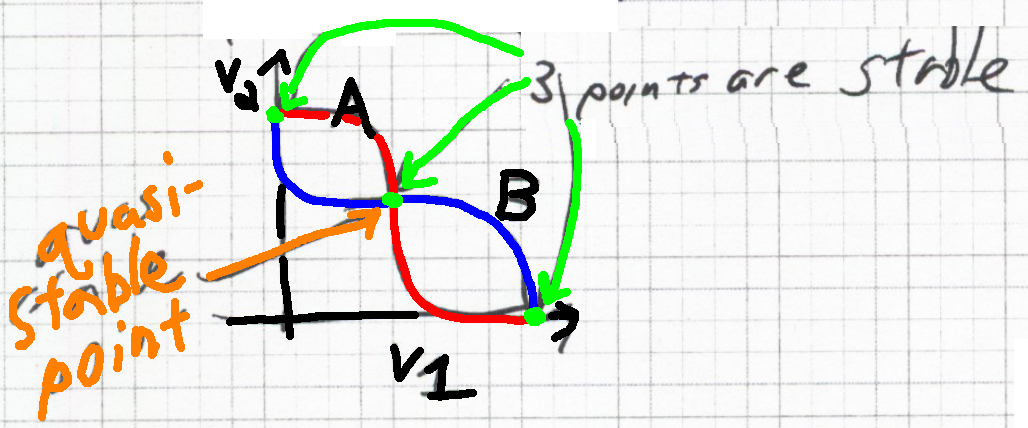
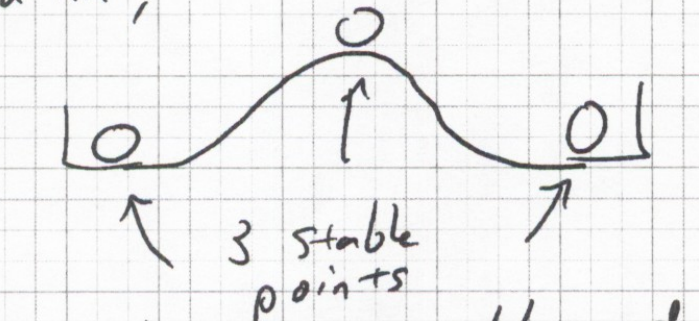
Three Points are possible solutions to both constraints
1 is a quasi stable solution
Temporal Dynamics Analysis
Time analysis:
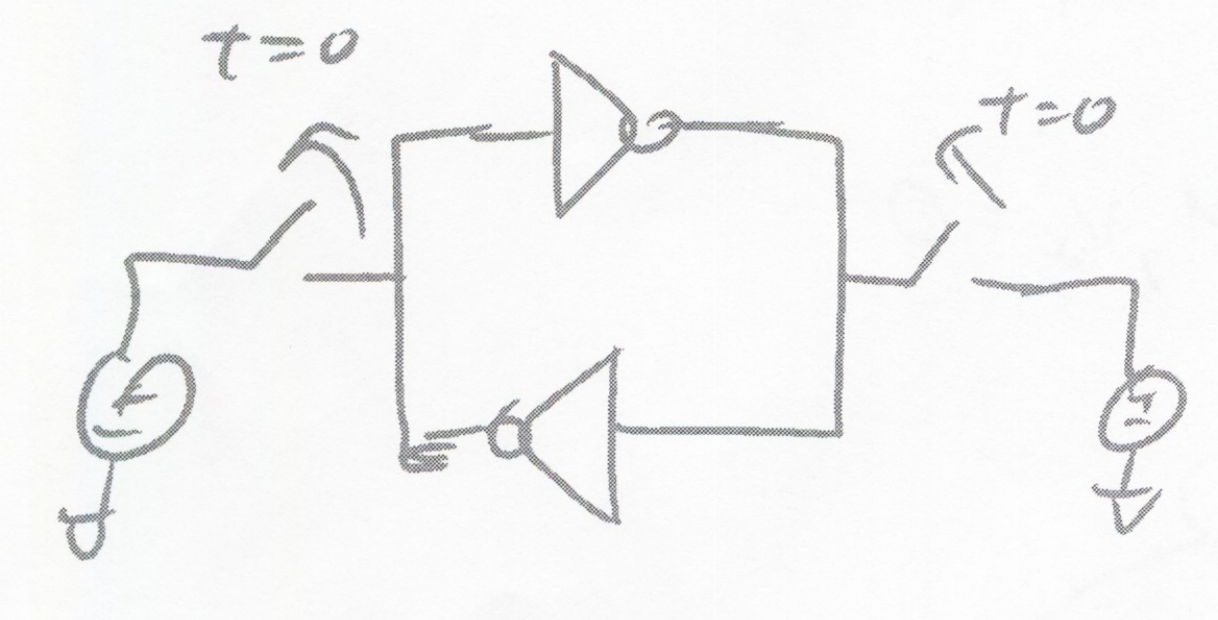
Consider ideal voltage sources and switches set two intial voltages
Switches are opened at time t=0
Case 1:
V1(0)=0
V2(0)=VDD
V1→0⇒A⇒V2→VDD⇒B⇒V1→0
Case 2:
V1(0)=VDD/2
V2(0)=VDD/2
V1→VDD/2⇒A⇒V2→VDD/2⇒B⇒V1→VDD/2
Case 3:
V1(0)=43VDD
V2(0)=41VDD
V1→43VDD⇒A⇒V2→0⇒B⇒V1→VDD
V1 is pushed to VDD, system stabalizes
@ (V1 = VDD, V2=0)
Case Quasistable:
In theory, the middle point is also stable
We have assumed a symmetric transfer function and constraints
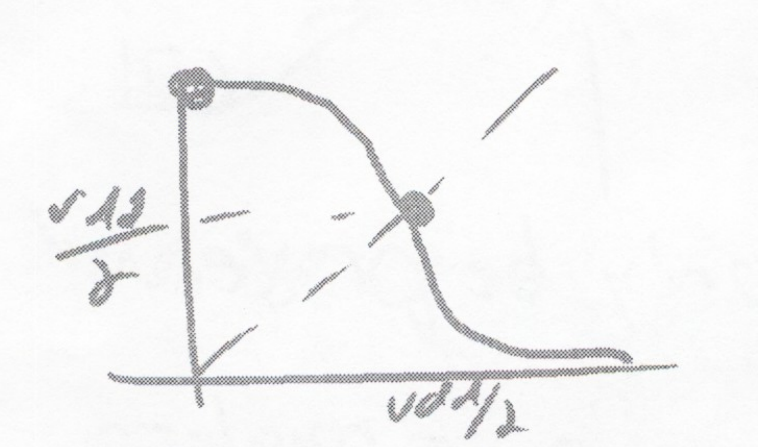
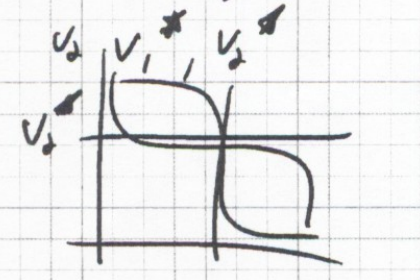
However, any noise will disrupt the balance.
If V1 is bumped more positive, V2 is pushed more negative and thus V1 is pushed more positive, etc...
Positive Feedback ensure until V1=VDD and V2=0
Quasi-stable
-
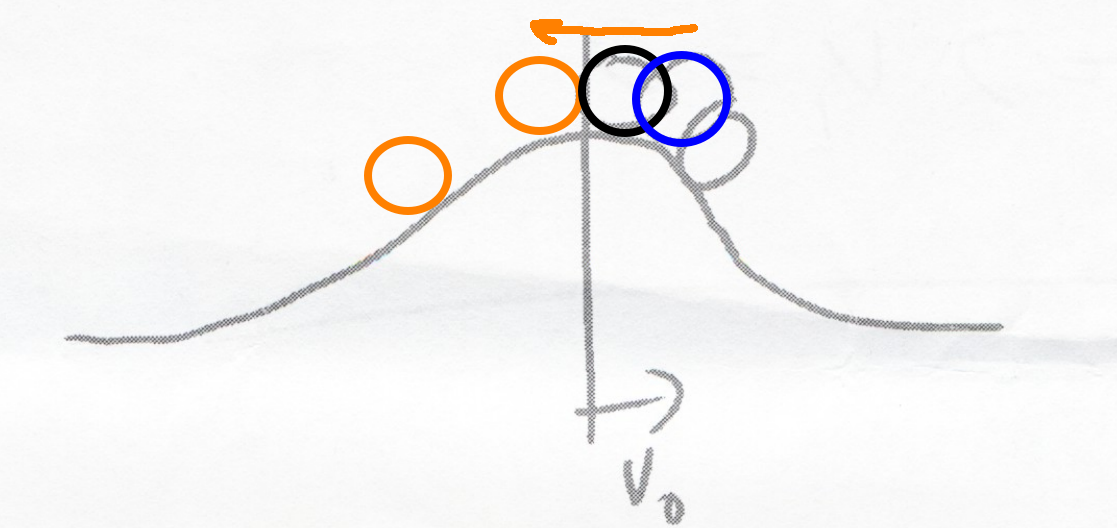
Think of of the quasi-stable point in the analogy of balancing a ball on a hill:
-
Middle point is quasistable and can only be preserved in a noiseless system. Starting points to the left of middle are pushed towards the left and starting points on the right are pushed to the right
-
Maintaining Highest Potential Energy:


Quasi-stable point can only be preserved in a noiseless system
Types of Memories
First consider for what types of memories this is relevant:
- Capacitor-Storage Based TODO: Draw a capacitor and switch
- Resistive (e.g. memristor) or other physical state changes
- Latch (Positive Feedback) Based
SRAM
Two Inverter (SRAM):
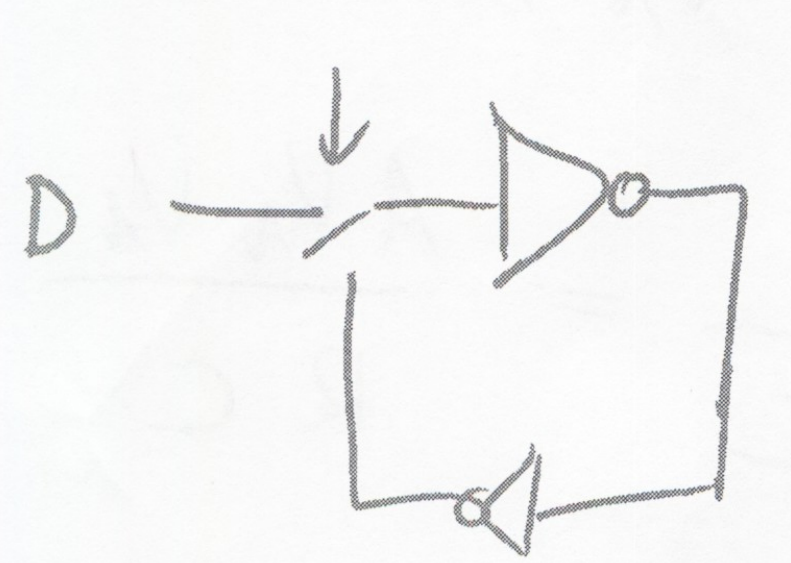
S-R Latch:
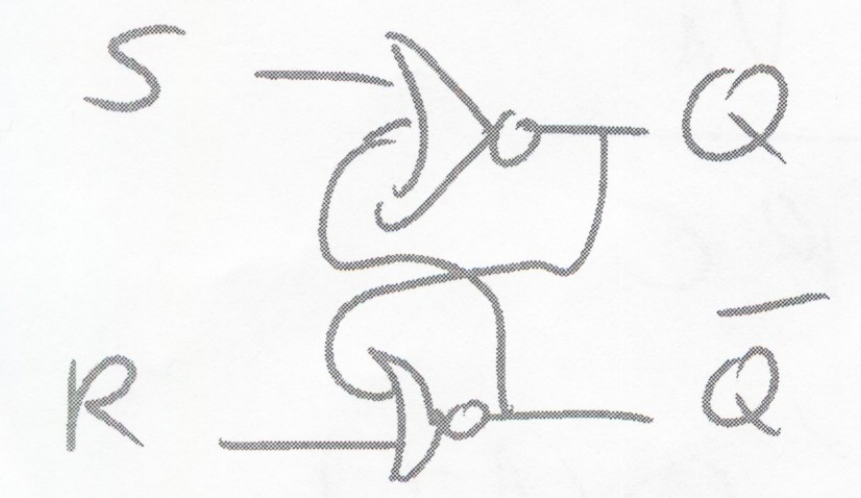
Clocked (Level Sensitive) SR Latch

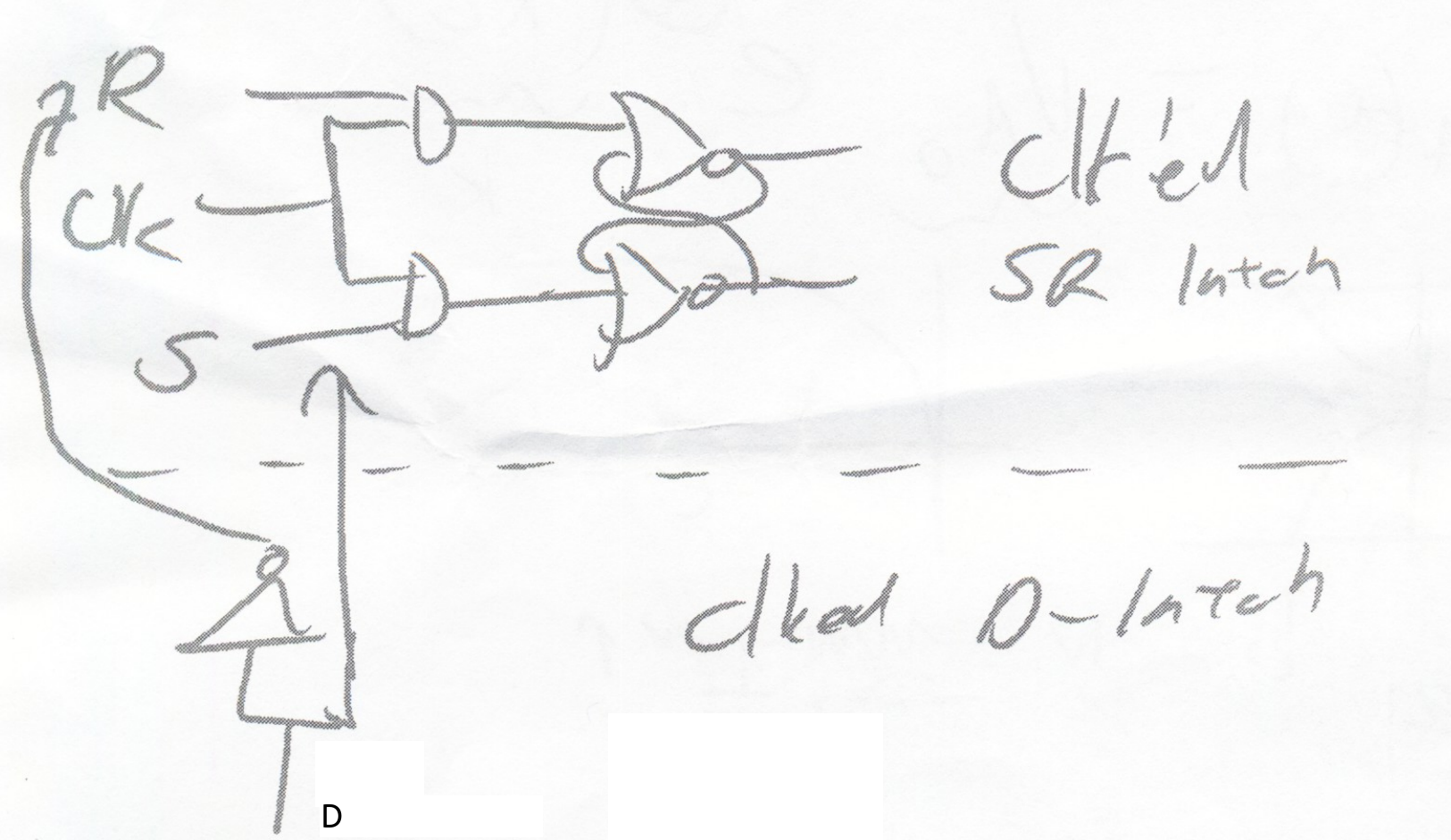
Clocked D-Latch:
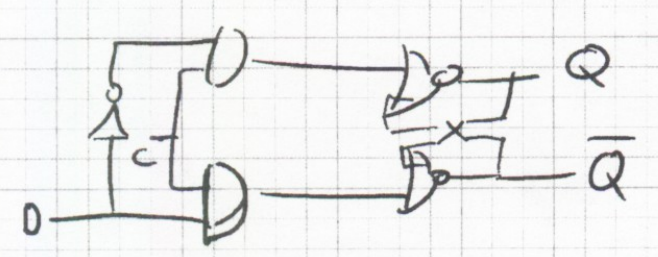
alternative view as extension of clocked SR latch:
Time to Settle

The question of interest is how long does is take to reach a stable state as a function of starting position?
Given VA(0) how long to reach a stable point?
Given T, a time limit to reach stable point, what is the constraint on VA(0)?
Metastable Cause
Clocked latches can be placed near a metastable state if the clock transistions while data is
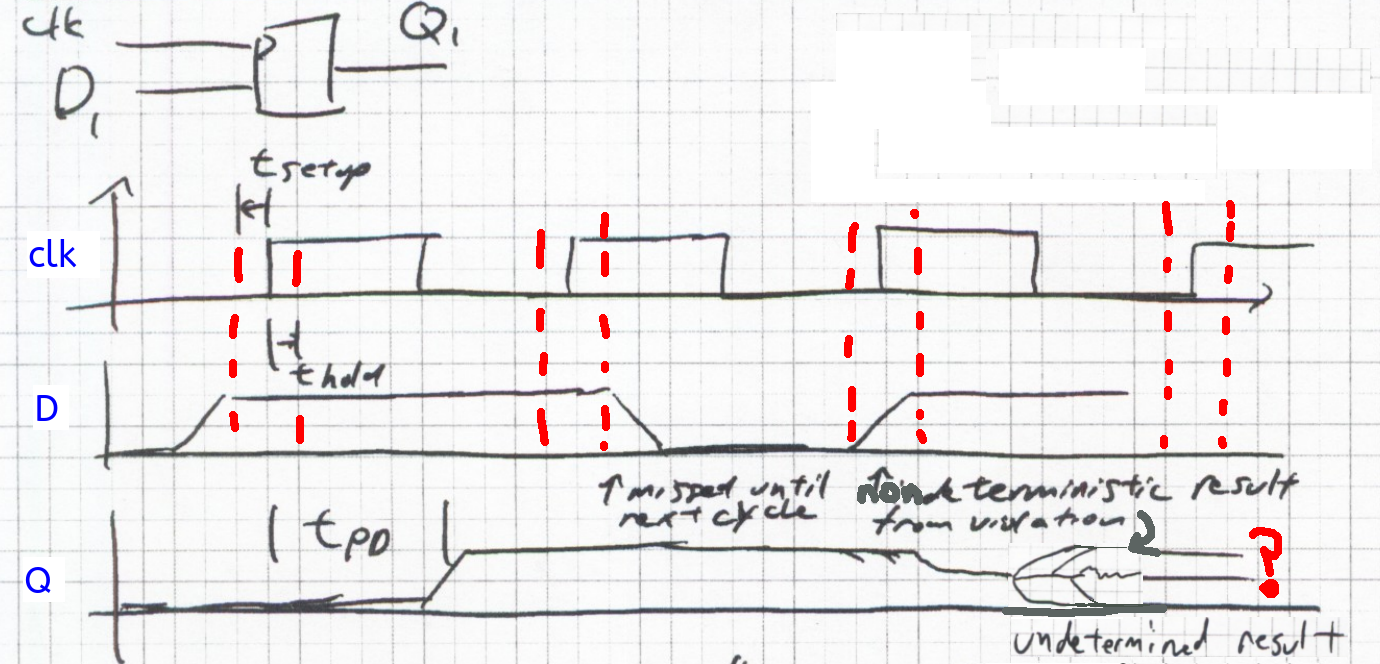
The problem is more than complex than "will it settle to the new or old value?"
If placed in a metastable state, the output can be stuck near the quasistable point for a very long time and the following stages will non-deterministically interpret the signal as 1 or 0 depending on thesholds and noise
- Latches are vulnerable to corruption when they are in a state near the quasi-stable point
- Transitions disrupted at the wrong time can be delayed reversed, or even undergo multiple transitions
Synchronized Input Capture:
Assume in the Logic, D1 and D2 represent two conditions that are normally never true but are often opposite in value. This logic is checking if the condition that D1 and D2 are ever true together
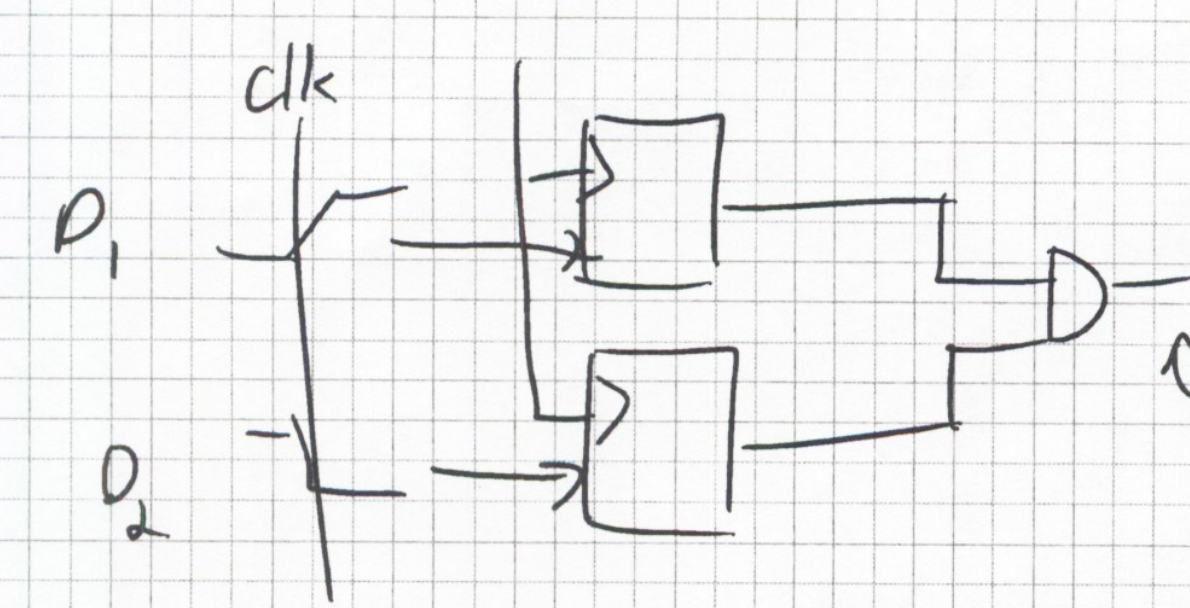
Here the output may glitch or become high in error under normal conditions, such as simutanuous tranistions D1:0→1 and D2:1→0
Resolution Fanout Point
At some point in the system, parallel resolution must happen that can cause a problem
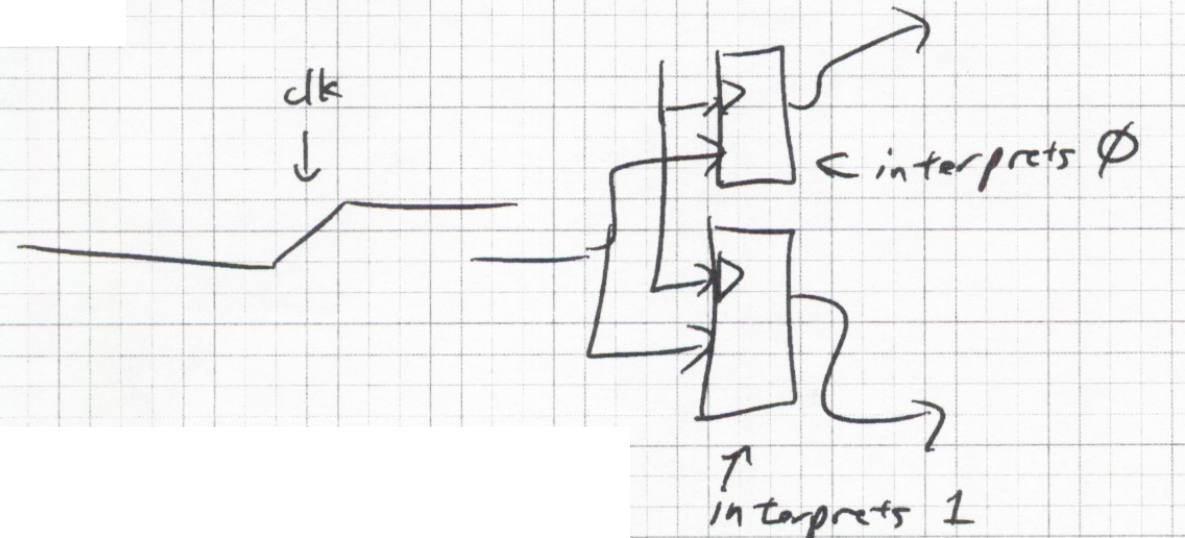
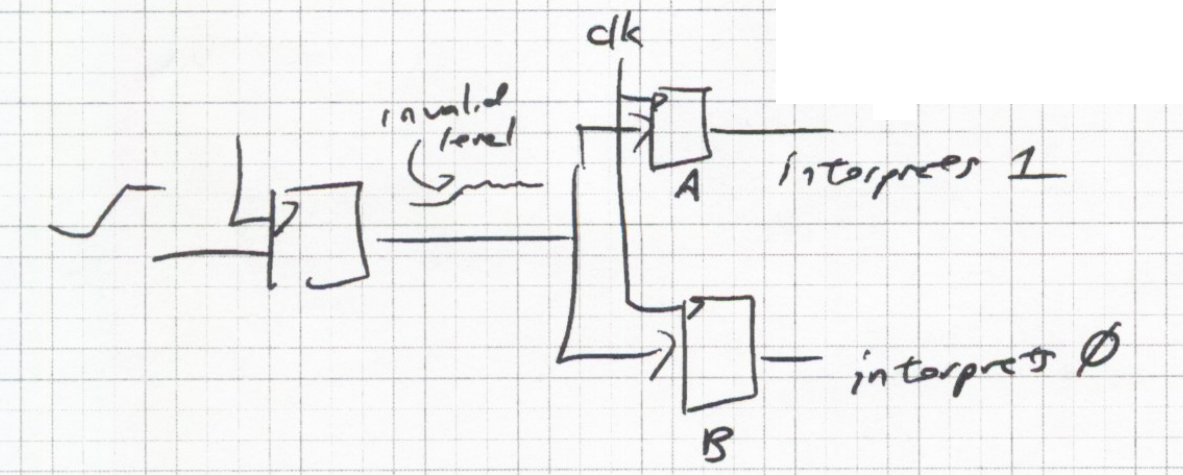
The same input signal (staring point) can be resolved differently in two components
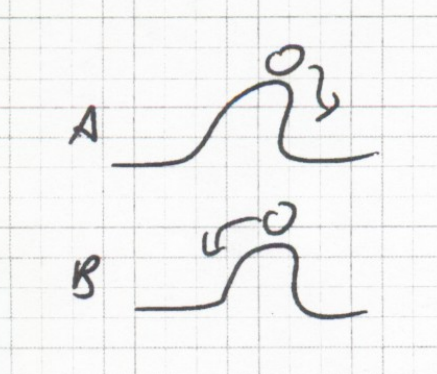
Temporal Analysis
A generic representation of positive feedback:
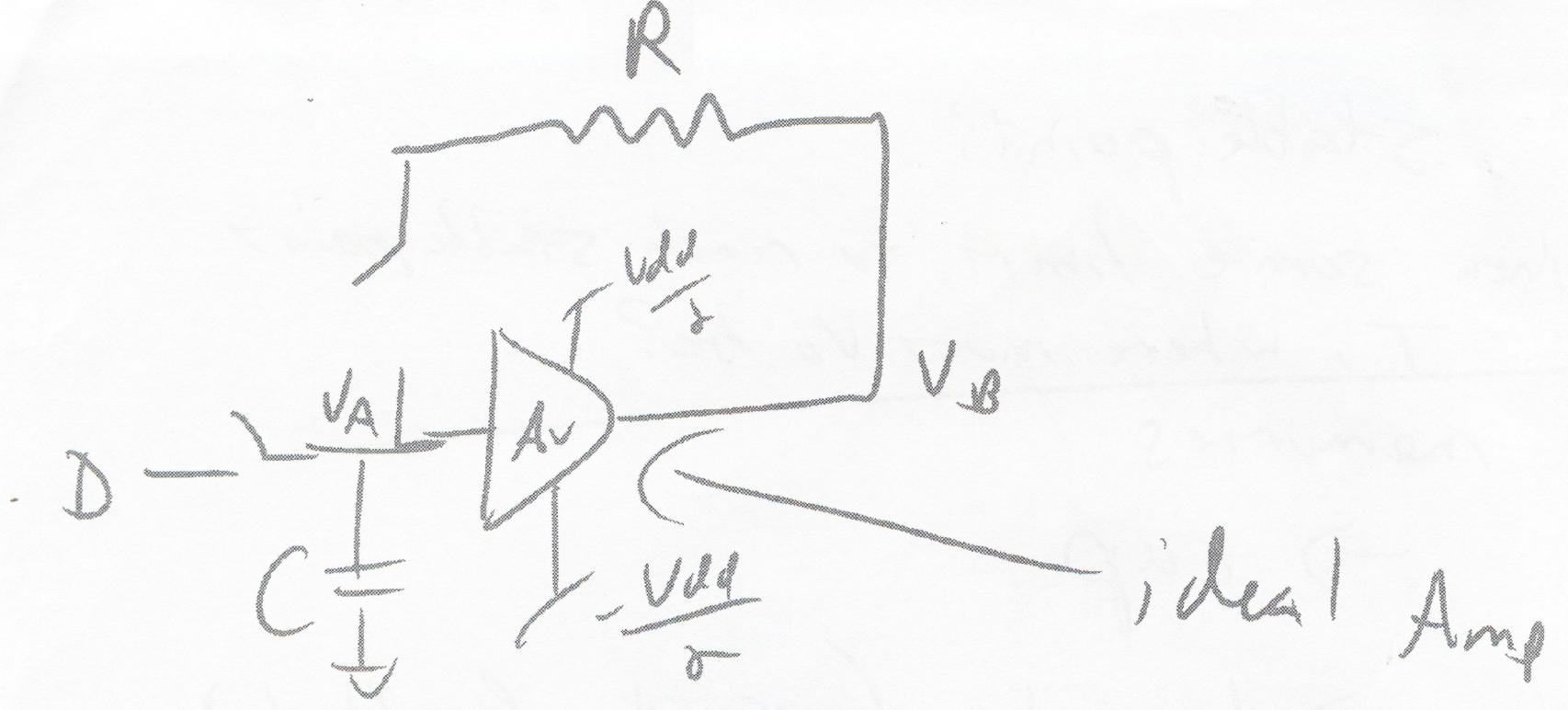
Assume the Ideal Amp, at all times VB=VA⋅A
Positive Feedback
General behaviour of positive feedback is to accellerate away from a quasi stable point (VA=VB=0)
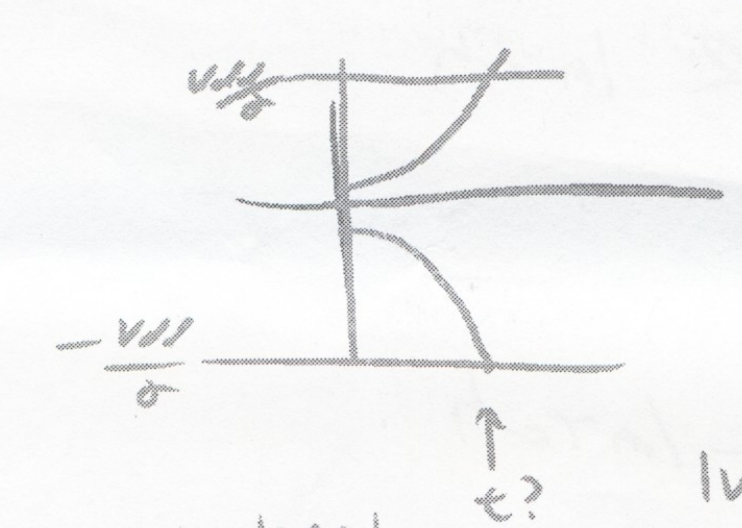
Negative feedback for comparison:
fast than slow settle at a equilibrium
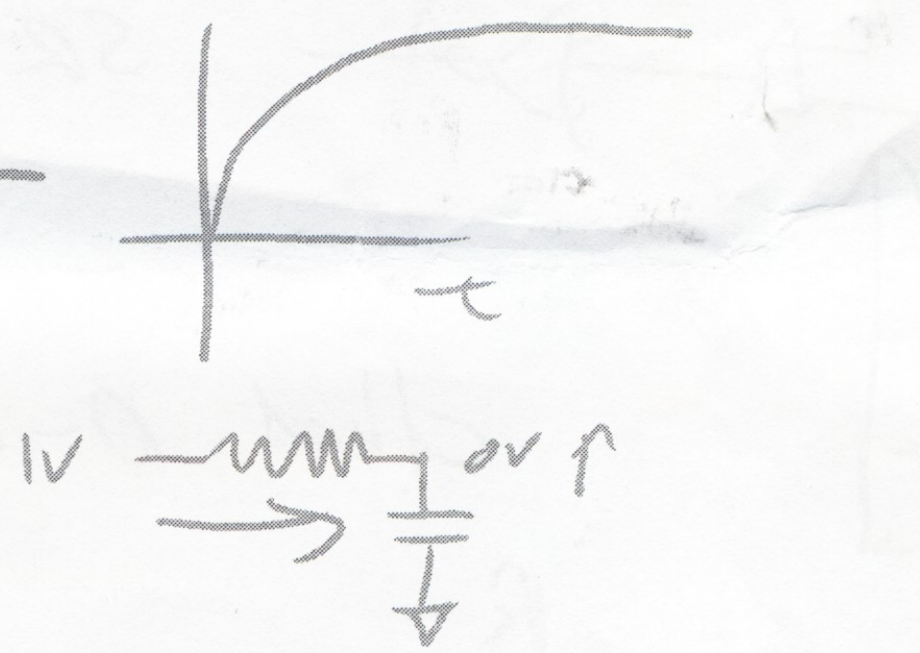
Analysis

Analyze the temporal voltage change at the input storage capacitor. The voltage value here represents the state of the system
dtdVA=CI=R⋅CVB−VA=R⋅CAVA−VA
dtdVA=R⋅C(A−1)VA
VA(t)=VA(0)etKRCA−1

The Question:
Time to reach VDD/2 ?
The Answer:
Approach:
Solve for t in VA(t)=VDD/2
t=K1ln(VA(0)VDD/2)
This is the time to reach VDD/2 given some starting point VA(0)
Time and Voltage Constraint
Bound t to be less than a desired clk-to-Q, i.e. time to resolve, Tr , and find ∣VA(0)∣min
Tr=K1ln(VA(0)VDD/2)
VA(0)=±(VDD/2)−1eTrK
Tr and VA(0) here represent the time and voltage constraints on the input

-
Starting values farther from the metastable equilibrium than ∣VA(0)∣min will resolve quickly
-
Starting values closer to the metastable equilibrium than ∣VA(0)∣min will resolve in a much longer amount of time, and meanwhile are more susceptible to noise corruption
-
Nature of Exponentials (Self-similartity)
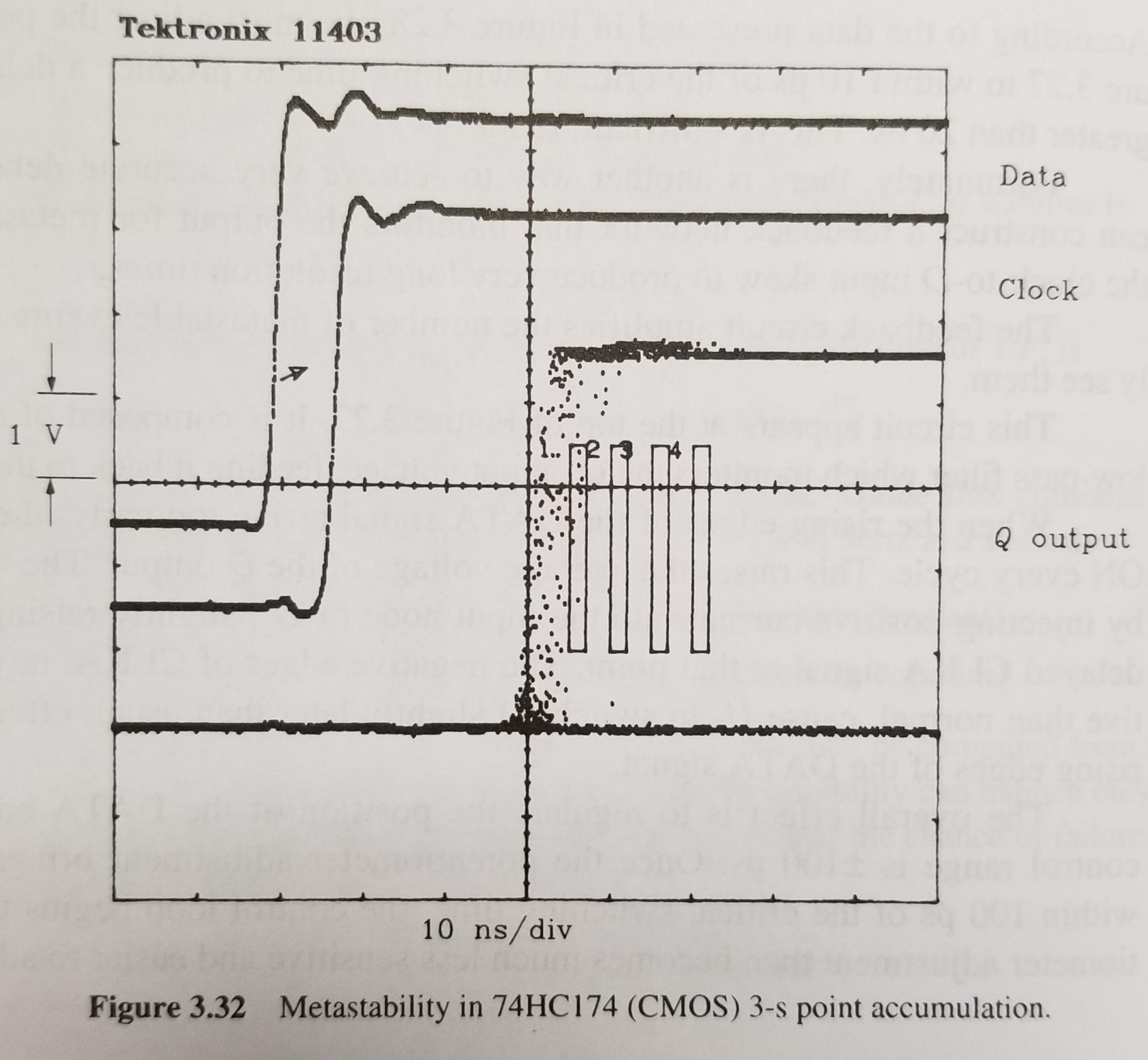
- Leads to linear input voltage -> exponential settling time relationship
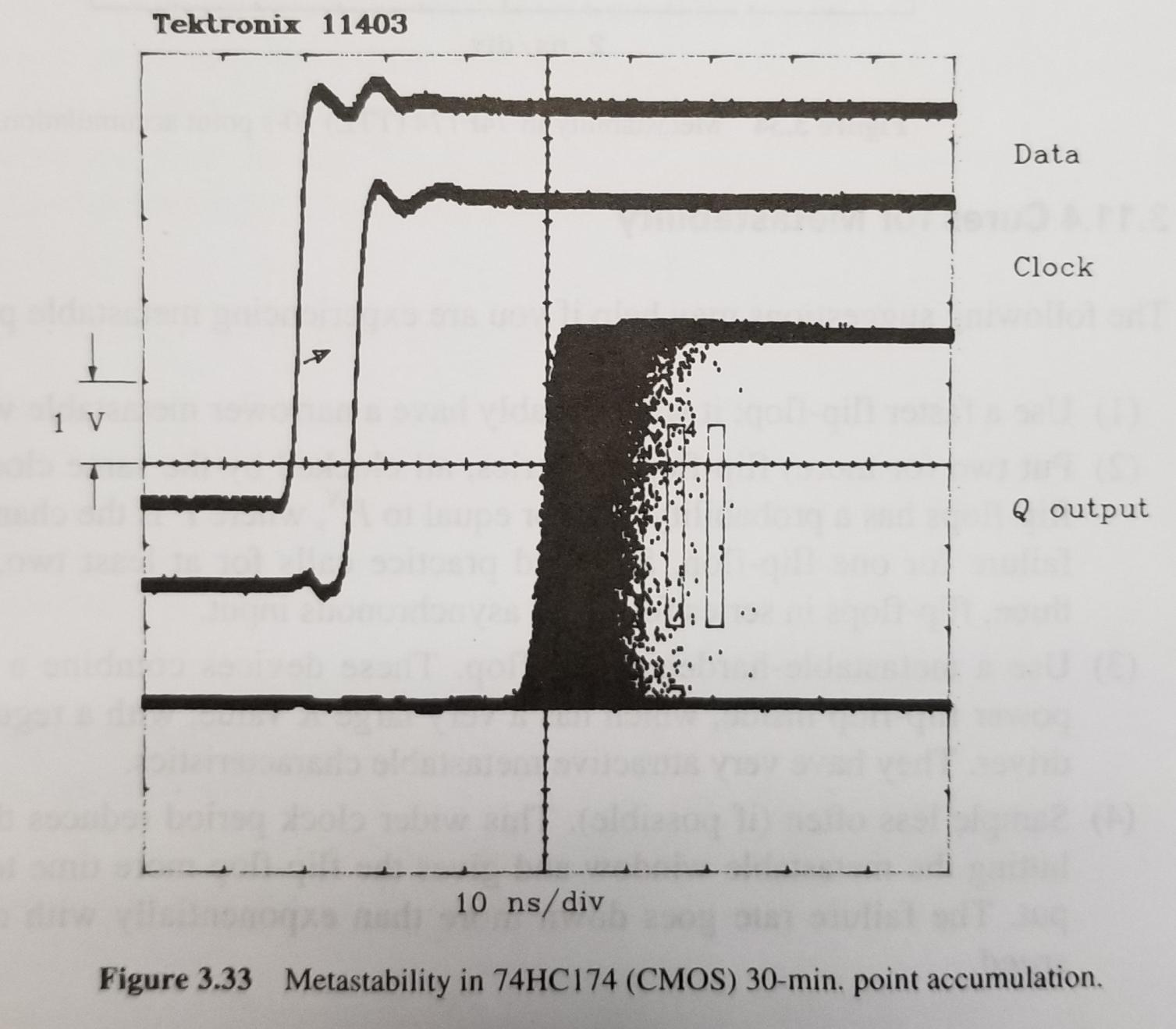
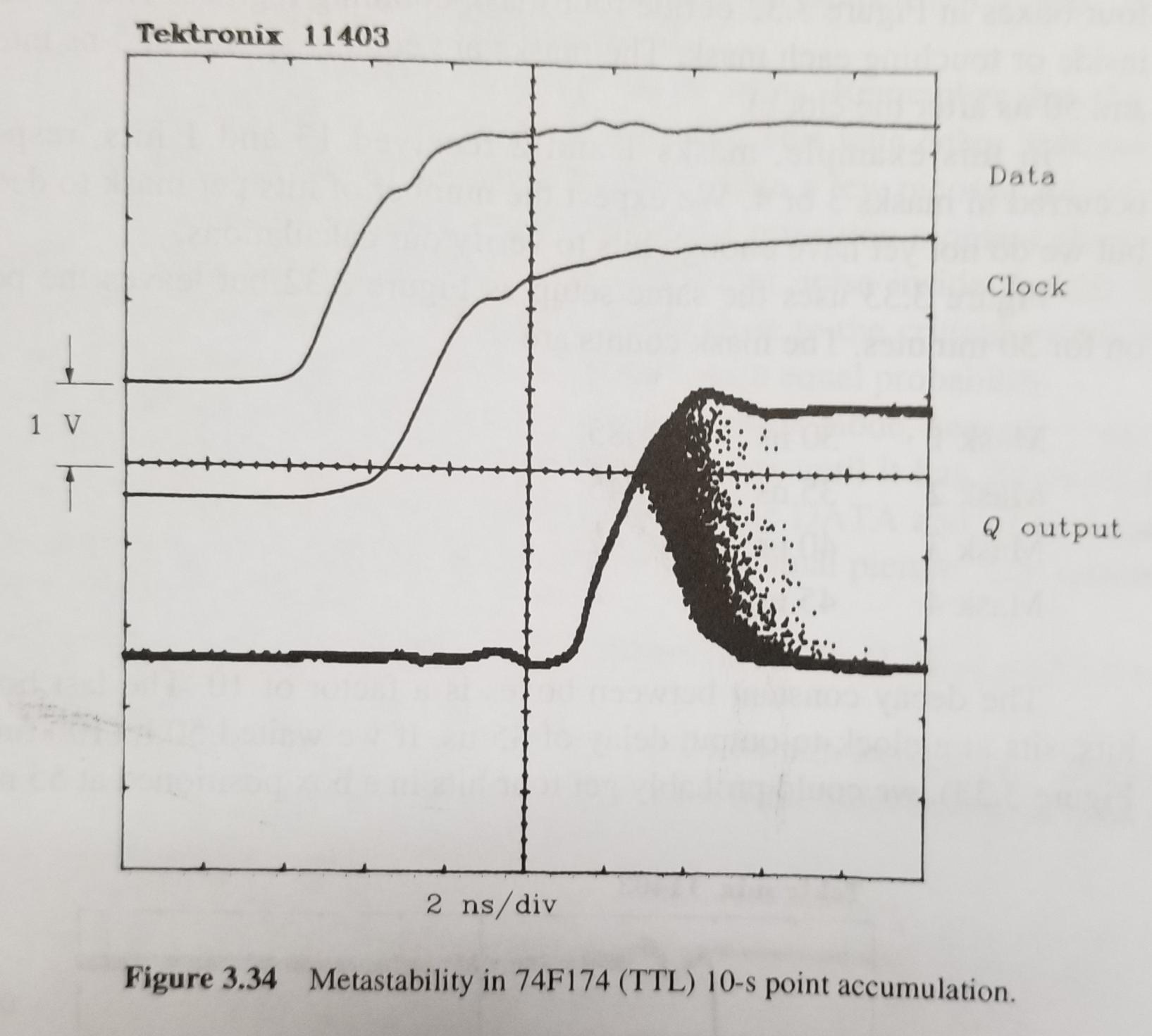
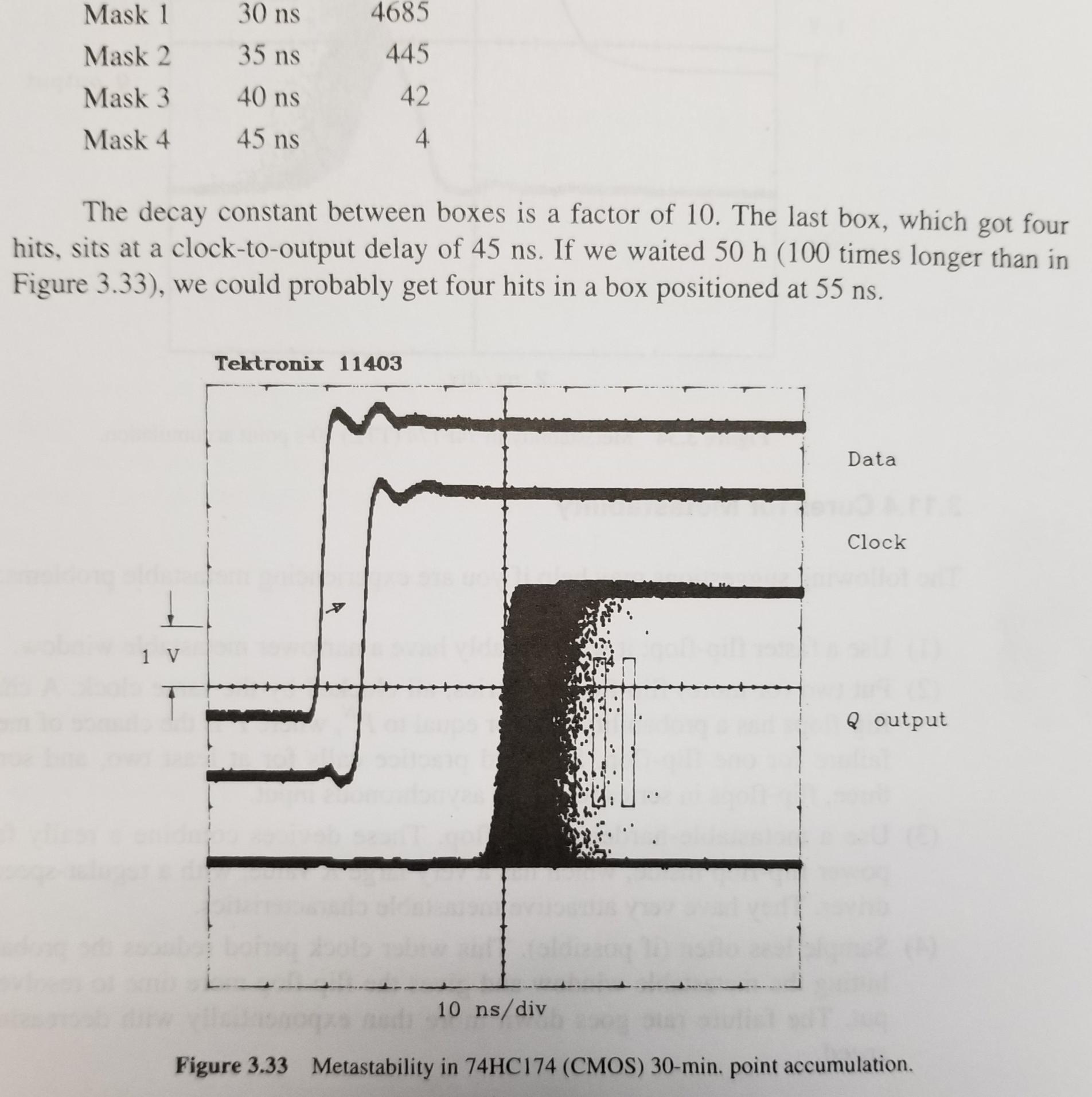
- See the mask counts on the next page for 30-min accumulation:
Implication of Metastabilty
For a given rise time, an input transition must stay outside a time window around the clock event
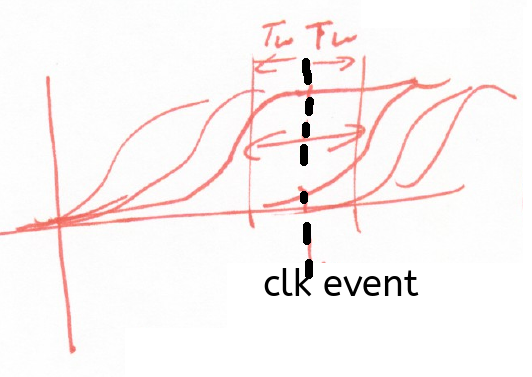
Implications of data transition slope and timing

The rise time and allowed arrival time of a 50% transition point are related
Data as Reference
For the next analysis: instead of viewing the clk as the reference and data timing as the variable:

We will switch and consider the data edge to be the transition
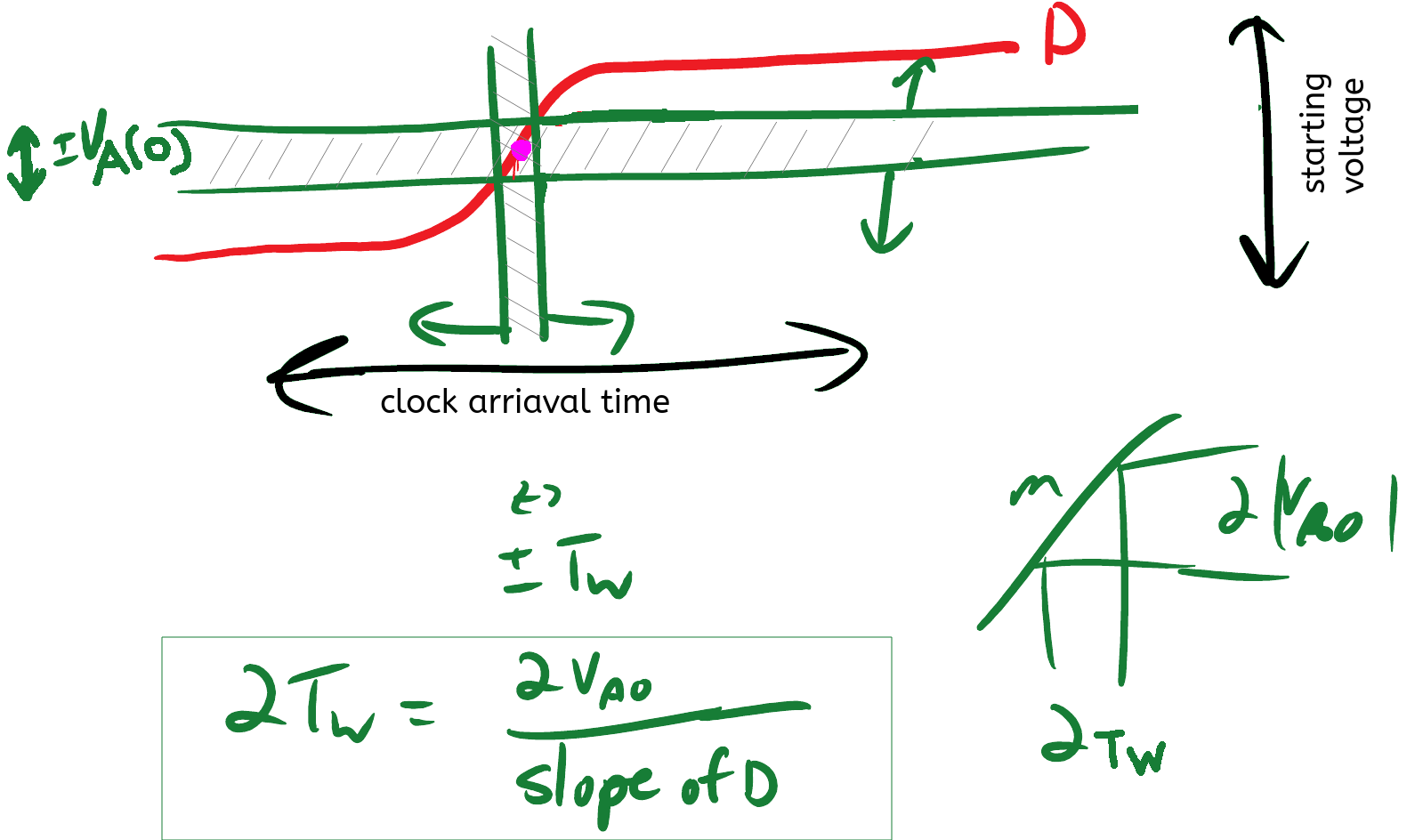
2∣TW∣≈T10−90VDD2VA(0)
2∣TW∣≈T10−90e−KTr
- If clock rises in in the data window, the output may not settle in time [eq 3.34]:
∣TW∣=Ce−KTr
- C is a constant (maybe found empirically), rise-time is a primary component
System Timing Requirements
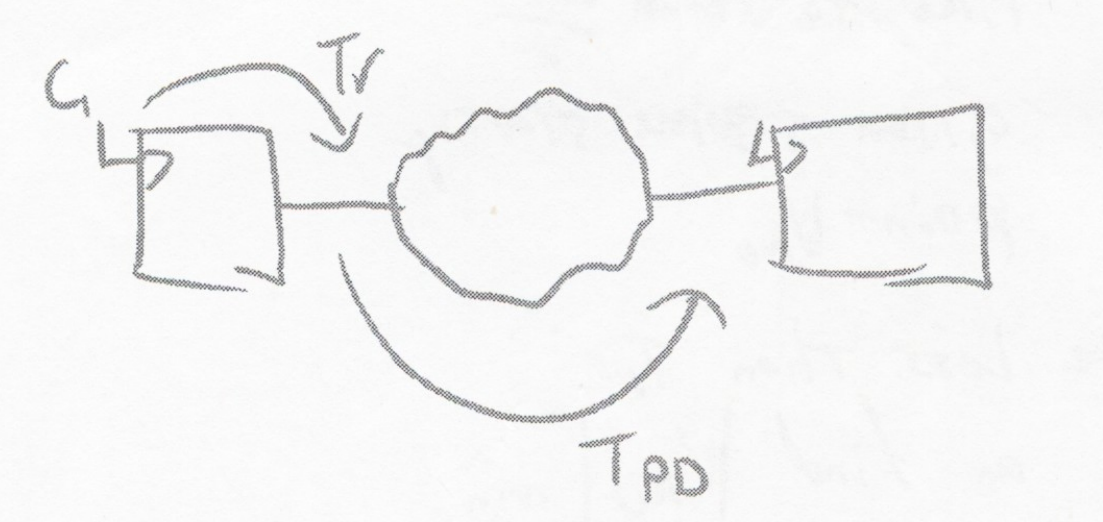
Tr<Fclk1−TPD→TW=Ce−KTr
TW is the window of error [eq 3.36] that helps define setup and hold time requirements and thus allowed combinatorial propagation delays
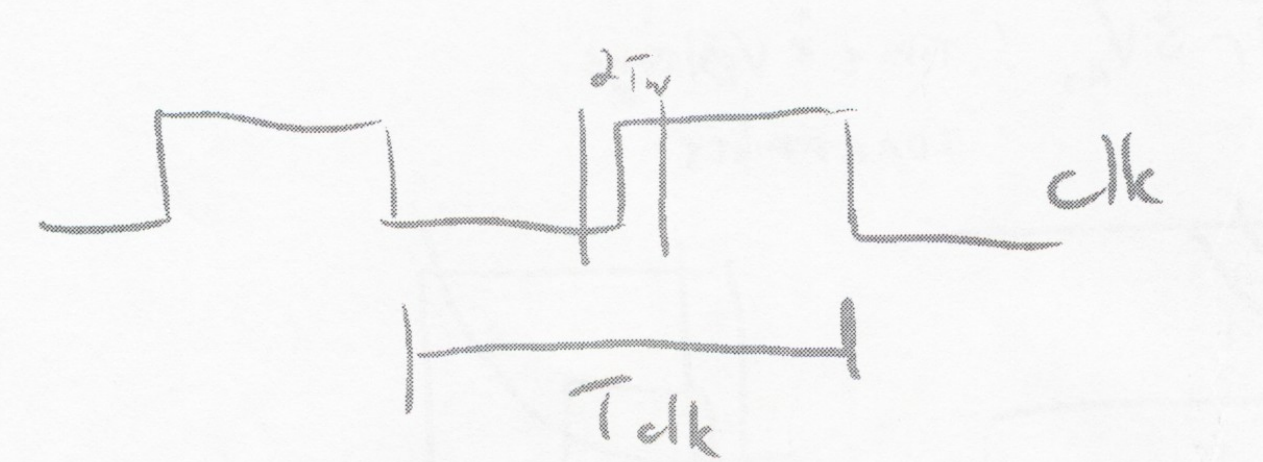
Operation Timeline
- Assume a uniformly random arrival of Data:
- Chance of MS Problem is [3.37]
- Probability of Failure Per Data Transition:
P=TCLK2TW=2FCLKCe−KTr
(this is the likelihood that a random transition falls in a disallowed epoch)
- Assume
- in given time span Tspan there are N data transitions expected
- each transition having probability P of causing a failure,
- The expected # of failures in that timespan
N⋅P failures in timespan Tspan
- The rate of failure is the rate of data transitions times the probability of a given transition causing a failure
TspanN⋅P=ExpectedRateofFailure
Mean Time Between Failures
-
The Rate of Failure is INVERSELY RELATED TO the mean time between failures
MTBF=R⋅P1;R=TspanN
R is the data transition rate
- When looking at various documents and datasheets, you may see many alternative forms but with similar underlying form
Actel 1989 ACT-1 Logic:
- Sample Switch Rise Time Constant C=.5×10−9
- Response Time Constant K=4.6052×109
Page 127
R (rate of transitions) is 1/10th of the clock rate
Mitigating Metastability
- Faster FF, naturally has narrowed metastability window
- N-FlipFlops in a row:
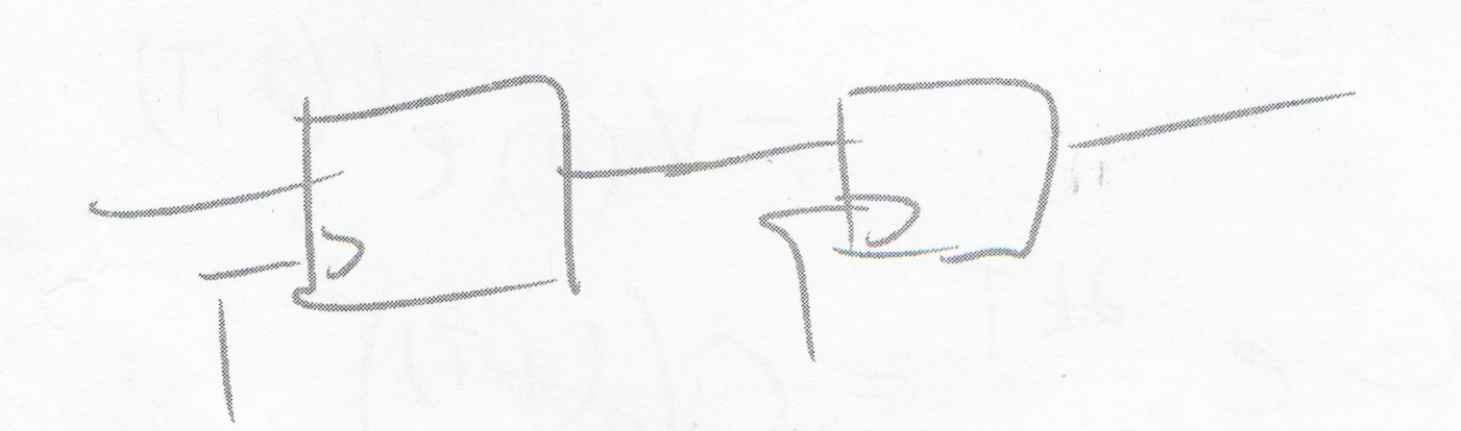

Effective Time provided is doubled (2T):
V3(2T)=V3(T)V2(T)updateeKT=V1(0)eKTeKT=V1(0)eK2T
TW=Ce−2KT=C(e−KT)2
Pfail∝TW1
Pfail=C1K21 for 2 flip-flops
Pfail=C1KN1 for N flip-flops
Another Possibility to realize this effect for a multi stage (e.g. master-slave) flip-flop:
-
Metastability-Hardened FF (rather than just a use higher-power fast FF, it would be a low-power flipflop specifically designed with large K)
-
Sample Less Often (Sacrifice Responsiveness)
-
Use Edge-Sharpening Amplifiers at the Input (Fast Transitions)