Managing Metastabilty in Systems
Ryan Robucci
• ESC/O-Key to see slide overview • ? to see help
References
- ꭝ
Metastability is Unsolvable
- Synchronization and Arbitration (overview and motivate metastability with arbitration problem) “Synchronization, Metastability and Arbitration”
- Understand Folk lure slides Page 16

- We can apply this general “two async” signals scenario to the specific situation where C is the clock and we want B to be data.
- Metastability is fundamentally not solvable (except for in special cases)
- Though the arbitration problem is unsolvable, special cases exist when the relation between B and C is constrained (meet certain timing analysis constraints) and the problem can be nearly practically avoided.
- Synchronous digital design practically avoids this problem between by ensuring that data does not change near a clock edge
- A special case of a multi-clock domain example is when one clock is an integer multiple of the the other
- Additional Material (not required) discussing some special cases of synchronization: https://cseweb.ucsd.edu/classes/wi06/cse291-b/slide/let4/timingint.pdf
- discussion on Classes of Metastability Problems depending on periodicity/clocking assumption of each signal and relationship of multiple clocks
Synchronizers in Digital Input Circuitry (microcontroller):
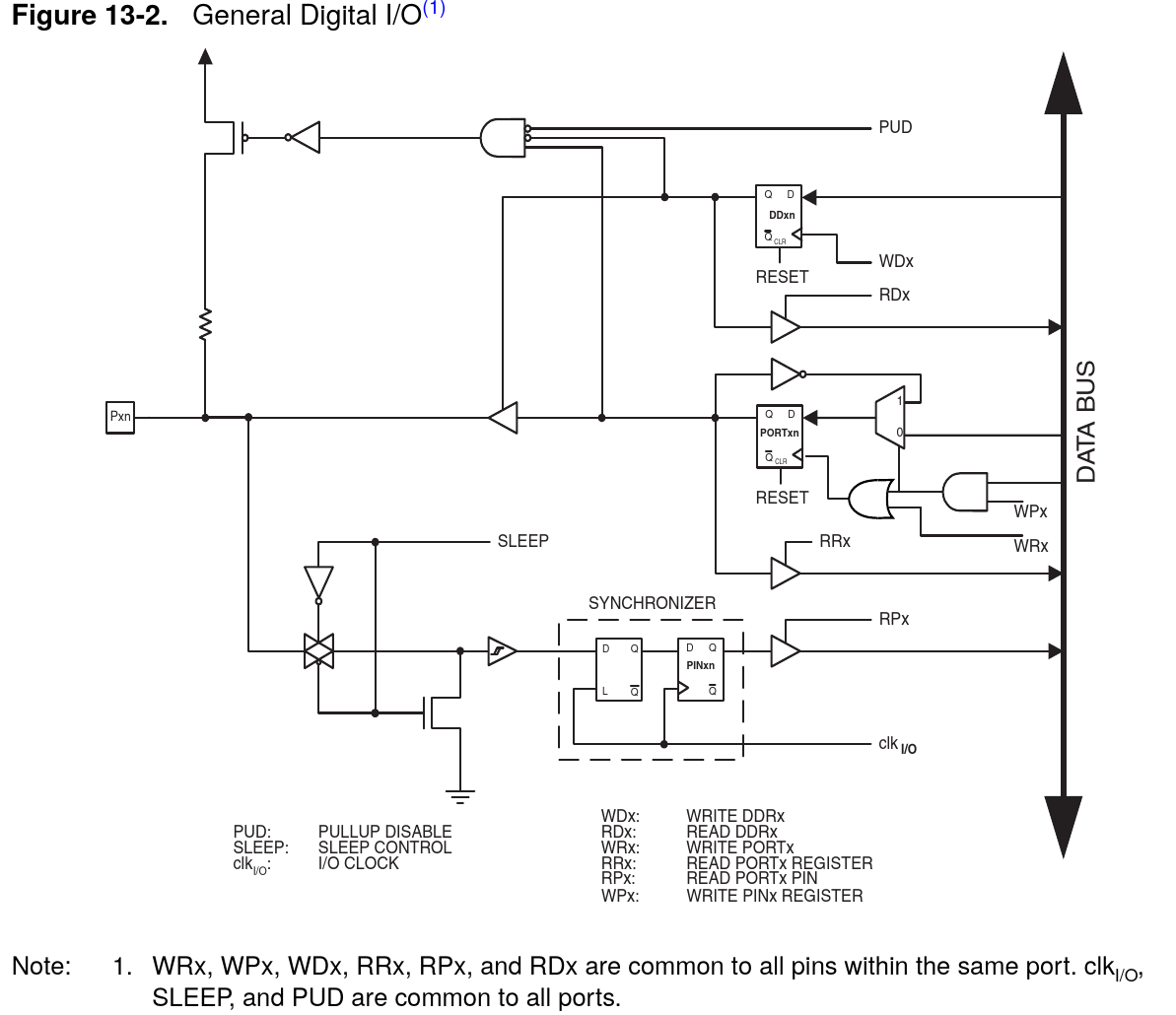
Note the use of a synchronizer in the following datasheet:
ww1.microchip.com/downloads/en/DeviceDoc/doc8018.pdf#page=66
FIFO as Synchronizers
- It is commont to use FIFOs to transfer data between clock domains (or to/from an asynchronous domain and a synchronous domain)
- IP Blocks and Generators are typically provided for this and are designed for metastability mitigation:
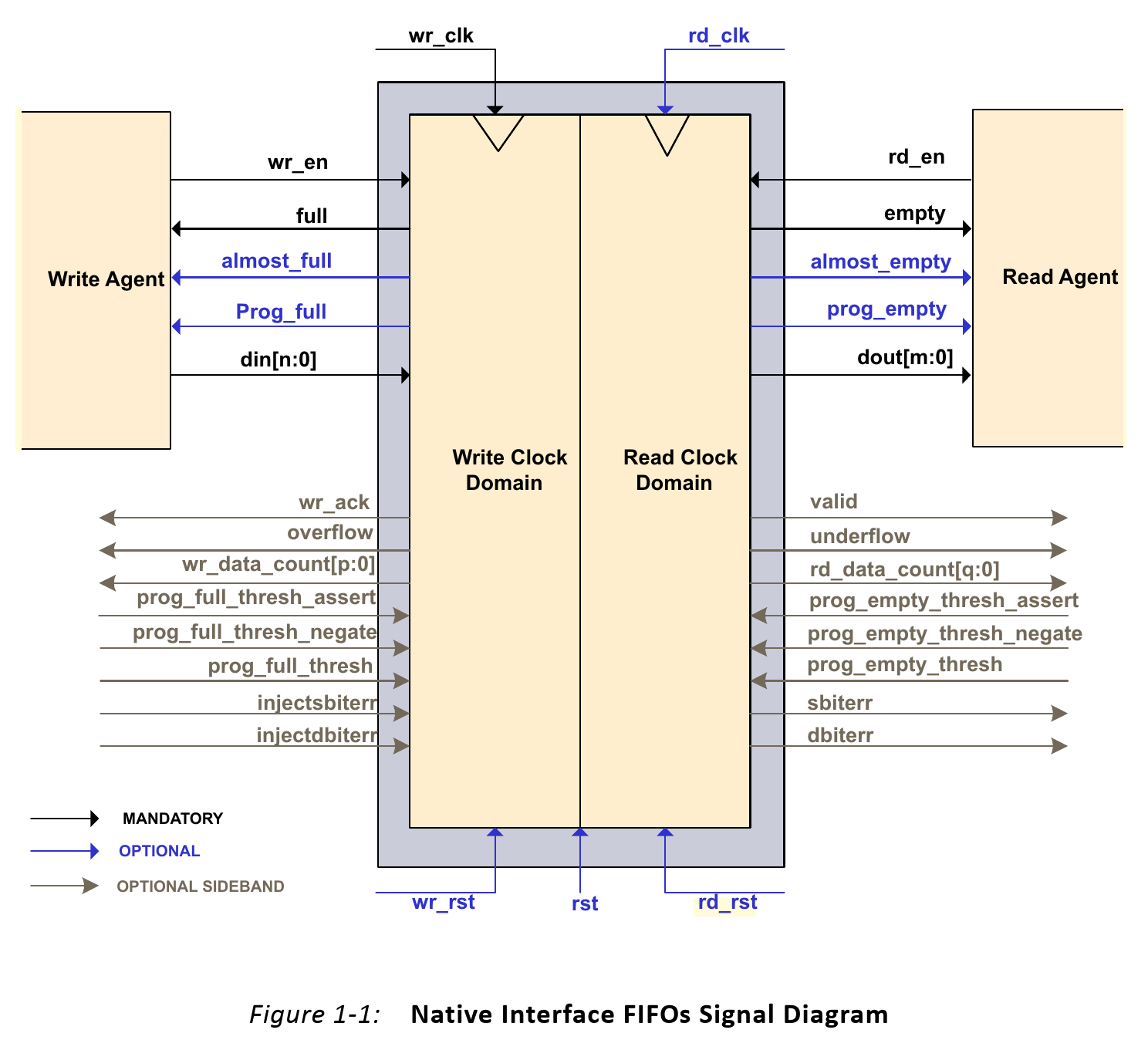

Understanding Metastability in FPGAs
-
In class overview document and especially page 5 for new material (next slide)
Understanding Metastability in FPGAs ꭝ -
While metastability wasn’t as much a concern for a while, modern lowering of supply voltages increased design sizes (with more chains) and increased data rates are cause for concern especially in life-critical applications.
ꭝ Page 5:
FPGA Architecture Enhancements
The metastability time constant C2 in the MTBF equation depends on various factors related to the process technology used to manufacture the device, including the transistor speed and the supply voltage. Faster process technologies and faster transistors allow metastable signals to resolve more quickly. As FPGAs have migrated from 180-nm process geometries to 90 nm, the increase in transistor speed usually improves metastability MTBF. Therefore, metastability has not been a major concern for FPGA designers.
However, as the supply voltage reduces with reduced process geometries, the threshold voltage for the circuit does not decrease proportionally. When a register goes metastable, its voltage is approximately one-half of the supply voltage. With a reduced power supply voltage, the metastable voltage level is closer to the threshold voltage in the circuit. When these voltages get closer together, the gain of the circuit is reduced and the registers take longer to transition out of metastability. As FPGAs enter the 65-nm process geometry and lower, with power supplies at 0.9V and lower, the threshold voltage consideration is becoming more important than the increase in transistor speed. Therefore, metastability MTBFs generally get worse unless the vendor designs the FPGA circuitry to improve metastability robustness.
Altera uses metastability analysis of the FPGA architecture to optimize the circuitry for improved metastability MTBF. Architecture improvements in Altera’s 40-nm Stratix ® IV FPGA architectures and new device development have improved the metastability robustness results by reducing the MTBF C2 constant.
MTBF and Timing Slack
- Timing slack is the amount of extra time a circuit has to setting according to timing analysis.
- Though sometimes it just excess, wasted time, it can have value mitigating metastability
- Extra slack represents extra time to resolve metastable conditions and can reduce failure rates beyond what a manufacturer has determined to be “acceptable to most”.
- Physical constraints tests should not always be thought of as having a binary outcome interpretation (Fail/Pass), sometimes “failing” simplified physical constraints a little is OK if you understand the impact, and passing with excess can have additional benefits.
ꭝMetastability in Altera Devices Page 5:
Design Optimizations
- "The exponential factor in the MTBF equation means that an increase in the design-dependent tMET [time to settle] value increases a synchronizer MTBF exponentially."
- Assume C2 is 50 ps:
- 200 ps increase in tMET makes the exponent 200/50 and increases MTBF by exp(4) (more than 50 times)
- 400 ps increase multiplies MTBF by exp(8) (almost 3k)
-
Considering a design with little timing slack and poor MTBF, slowing the clock little (200 ps) can have valued impact (fclk=500MHz↔fclk=2000ps)
-
For a design with a large amount of timing slack, the reduction in MTBF may not be of value
-
Page 4 discuss MTBF Plot
-
Brief on Xilinx (discuss “extra” delay”)
MTBF with Multiple Points of Failure
- When considering multiple chains in a system, calculating overall MTFB is done by converting “back” to failure rate FR using inverse, summing rates and inverting back.
- FR=FR1+FR2+FR3+…+FRN
MTBF1=MTBF11+MTBF21+MTBF31+…+MTBFN1
MTBF=MTBF11+MTBF21+MTBF31+…+MTBFN11 - As a result, the lowest MTBF tends to define the MTBF for the system (if it helps, recall that the upper bound on parallel resistances is the lowest resistance)
ꭝMetastability in Altera Devices Page 5:
- The path with the worst MTBF has a major affect on the design MTBF
- Consider two different designs that have ten synchronizer chains.
- ten chains with the same MTBF of 10,000 years
- MTBF is sum of the failure rates for each chain (failure rate is 1/MTBF); metastability failure rate of 10 chains × 1/10,000 years = 0.001, therefore the design MTBF is 1000 years.
- nine chains with MTBF of a million years but one chain with MTBF of 100 years
- failure rate of 9 chains × 1/1,000,000 + 1/100 = 0.01009 and the design MTBF is about 99 years—just slightly less than the MTBF of the worst chain.
Review In-Class:
Synthesis and Scripting Techniques for Designing Multi-
Asynchronous Clock Designs (2001)
http://www.sunburst-design.com/papers/CummingsSNUG2001SJ_AsyncClk.pdf
Details of Code for FIFO implementation shown at end of 2001 paper:
Simulation and Synthesis Techniques for Asynchronous
FIFO Design (2002)
http://www.sunburst-design.com/papers/CummingsSNUG2002SJ_FIFO1.pdf
Interview Questions
https://www.glassdoor.com/Interview/uk-digital-design-engineer-interview-questions-SRCH_IL.0,2_IN2_KO3,26.htm
Cisco: Clock domain crossings in cases where very fast sending signals arriving at a much slower clock domain. How to capture without losing any incoming signal event into the slow clock domain? No idea as to how frequent or how long incoming events appear.
Apple Interview Question:
https://www.glassdoor.com/Interview/Describe-how-a-multi-bit-synchronizer-async-fifo-handles-the-variable-delay-of-each-bit-QTN_1243086.htm