Signed Integers and Arithmetic
Ryan Robucci
• ESC/O-Key to see slide overview • ? to see help
Signed and Unsigned Integers
Consider n ordered bits representing a value X
Unsigned Interpretation:
i=0∑n−1(xi2i)=
xn−12n−1+i=0∑n−2(xi2i)
Signed Interpretation (MSB used for representing Negative Numbers)
−xn−12n−1+i=0∑n−2(xi2i)
-
If MSB, xN−1 , is 0
- unsigned: X<=2N−2−1
- signed: X positive
- the interpretation is the same
-
If MSB, xN−1 , is 1,
- unsigned: X>=2N−1
- signed: X negative
- the interpretation is different
- Interpreting unsigned as signed:
- Reinterpreting (1)2N−1 as −(1)2N−1 means subtracting 2N
- Interpreting signed as unsigned:
- Reinterpreting −(1)2N−1 as (1)2N−1 means adding 2N
| Bits x3x2x1x0 |
Unsigned | Signed | |
|---|---|---|---|
0000 |
0 | = | +0 |
0001 |
1 | = | +1 |
0010 |
2 | = | +2 |
0011 |
3 | = | +3 |
0100 |
4 | = | +4 |
0101 |
5 | = | +5 |
0110 |
6 | = | +6 |
0111 |
7 | = | +7 |
1000 |
8 | →−16 | −8=24−8 |
1001 |
9 | ←+16 | −7=24−9 |
1010 |
10 | −6=24−10 | |
1011 |
11 | −5=24−11 | |
1100 |
12 | −4=24−12 | |
1101 |
13 | −3=24−13 | |
1110 |
14 | −2=24−14 | |
1111 |
15 | −1=24−15 |
Complement and Increment
- Negating in two’s complement: adding (and subtracting) signed and unsigned numbers is no different at the bit/hardware level, represented as modular arithmetic
X+Yis (X+Y)%2N2^N-Xis (2N−X)%2N=−X- However, 2N cannot be represented with N bits, but 2N−X can be represented in two operations
- Let Y=(2N−1)
- Then (Y−X)+1 which is ((Y−X)%2N+1)%2N=−X
- Ones complement is inverting bits: "ones"−X , arithmetically described as (2N−1)−X in modular arithmetic is (2N−1)−X%2N=−1−X
- Therefore, to implement negation we just add 1 to the complement
(2N−1)−X+1=2N–X
as modular arithmetic is
(2N−1)−X+1=(2N–X)%2=−X
Long/short unsigned/signed Conversion Rules
(C/C++) Combinations of (dest type) = (source type) to consider
( unsigned long) = (unsigned long)
( unsigned long) = ( signed long)
( signed long) = (unsigned long)
( signed long) = ( signed long)
(unsigned short) = (unsigned long)
(unsigned short) = ( signed long)
( signed short) = (unsigned long)
( signed short) = ( signed long)
( unsigned long) = (unsigned short)
( unsigned long) = ( signed short)
( signed long) = (unsigned short)
( signed long) = ( signed short)
(unsigned short) = (unsigned short)
(unsigned short) = ( signed short)
( signed short) = (unsigned short)
( signed short) = ( signed short)
- The C rules are “simple” and used in Verilog:
- extend or truncate source
- Going from longer to shorter, upper bits are truncated
- Going from shorter to longer, zero or sign extension is done
depending on source type being unsigned or signed respectively
- bit copy
- To/From signed/unsigned is just bit copying, no other smart manipulation/conversion/rounding is done
Long/short unsigned/signed Verilog Conversion Rule Demo
module conversion_demo; wire [7:0] u8x = 8'b11111111; wire signed [7:0] s8x = 8'b11111111; wire [15:0] u16x = 16'b1111_1111_1111_1111; wire signed [15:0] s16x = 16'b1111_1111_1111_1111;
wire [15:0] u16y_ux = u8x; wire [15:0] u16y_sx = s8x; wire signed [15:0] s16y_ux = u8x; wire signed [15:0] s16y_sx = s8x; wire [7:0] u8y_ux = u16x; wire [7:0] u8y_sx = s16x; wire signed [7:0] s8y_ux = u16x; wire signed [7:0] s8y_sx = s16x;
initial begin #0; $display("u16y_ux: %16b, %7d",u16y_ux,u16y_ux); //u16y_ux: 0000000011111111, 255 $display("u16y_sx: %16b, %7d",u16y_sx,u16y_sx); //u16y_sx: 1111111111111111, 65535 $display("s16y_ux: %16b, %7d",s16y_ux,s16y_ux); //s16y_ux: 0000000011111111, 255 $display("s16y_sx: %16b, %7d",s16y_sx,s16y_sx); //s16y_sx: 1111111111111111, -1
$display(" u8y_ux: %16b, %7d",u8y_ux,u8y_ux); //u8y_ux: 11111111, 255 $display(" u8y_sx: %16b, %7d",u8y_sx,u8y_sx); //u8y_sx: 11111111, 255 $display(" s8y_ux: %16b, %7d",s8y_ux,s8y_ux); //s8y_ux: 11111111, -1 $display(" s8y_sx: %16b, %7d",s8y_sx,s8y_sx); //s8y_sx: 11111111, -1 end endmodule
Summary of Points
- Two compliment addition of two N-bit numbers can require up to N+1 bits to store a full result
- Two’s compliment addition can only overflow if signs of operands are the same (likewise for subtraction the signs must be different)
- Result of N-bit addition with overflow is dropping of MSBits’s: A+B = (A+B) mod (2^N)
- For multiplication, multiplying two N-bit numbers requires up to 2N bits to store the operand. Multiplying a N-bit with a M-bit requires up to N+M bits.
Adder Structures
Discussed in Next Lecture
Sign Extension with Operations using Signed Variables
wire signed [11:0] x,y; wire signed [12:0] s1,s2; assign s1 = {8{x[7]},x} + {8{y[7]},y} //explicit sign extension assign s2 = x + y; //implicit sign extension
Signed Addition in Verilog
wire signed [7:0] x,y,s; wire flagOverflow; assign s = x+y; //context determined // 8-bit addition //overflow case is when the sign of the // input operands are the same and // sign of result does not match assign flagOverflow = (x[7] == y[7]) && (y[7] ~= s[7])
Rounding Errors -- float to int
- Conversion from float to int is defined as truncation of fractional digits, effectively rounding towards zero
- 5.7→5
- −5.7→−5
- Nearest Integer Rounding using Floating Point Biasing:
- Add +/- .5 before truncation depending on sign
- Positive Numbers:
- 5.7+.5=6.2→6
- 5.4+.5=5.9→5
- −5.7+.5=−5.2→−5 doesn’t work
- For negative numbers, need to subtract
- −5.7−.5=−6.2→−6
- −5.4−.5=−5.9→−5
Rounding errors
Assume int A,B;
- A/B gives floor(A/B) rather than round(A/B)
- So (A+B/2)/B is how we get rounding with integer-only arithmetic
- If B is odd, we need to choose to round B/2 up or down depending on application
Example:
- Want to set serial baud rate using clock divider
i.e.BAUD_RATE=CLK_RATE/CLK_DIV - Option 1:
#define CLK_DIV (CLK_RATE/BAUD_RATE)
- Option 2: BETTER CHOICE WITH INTEGER BIASING
#define CLK_DIV (CLK_RATE+(BAUD_RATE/2))/BAUD_RATE
Choices for order of operations
-
In general, if intermediate result will fit in the allowed integer word size, apply integer multiplications before integer divisions to avoid loss of precision
-
Need to consider loss of MSB or LSB digits with intermediate terms and make choices base on application or expected ranges for input values
-
Example 1:
int i = 660, x = 54, int y = 23;- want i/x*y : true answer is 255.555…
i/x*ygives 253 : good
i*y/xgives 255 : better
(i*y+x/2)/xgives 256 : best
- want i/x*y : true answer is 255.555…
-
Example 2:
unsigned int c = 7000, x=10,y=2;- want
c*x/ywhich is truly35000
c*=x;overflows c since(c*x)>65535resulting inx = 4465
c/=y;get2232here
c/=y; c*=x;gives35000!!!!!
- want
-
In general, if intermediate result will fit in the allowed integer word size, apply integer multiplications before integer divisions to avoid loss of precision
Limitations of Limited Precision
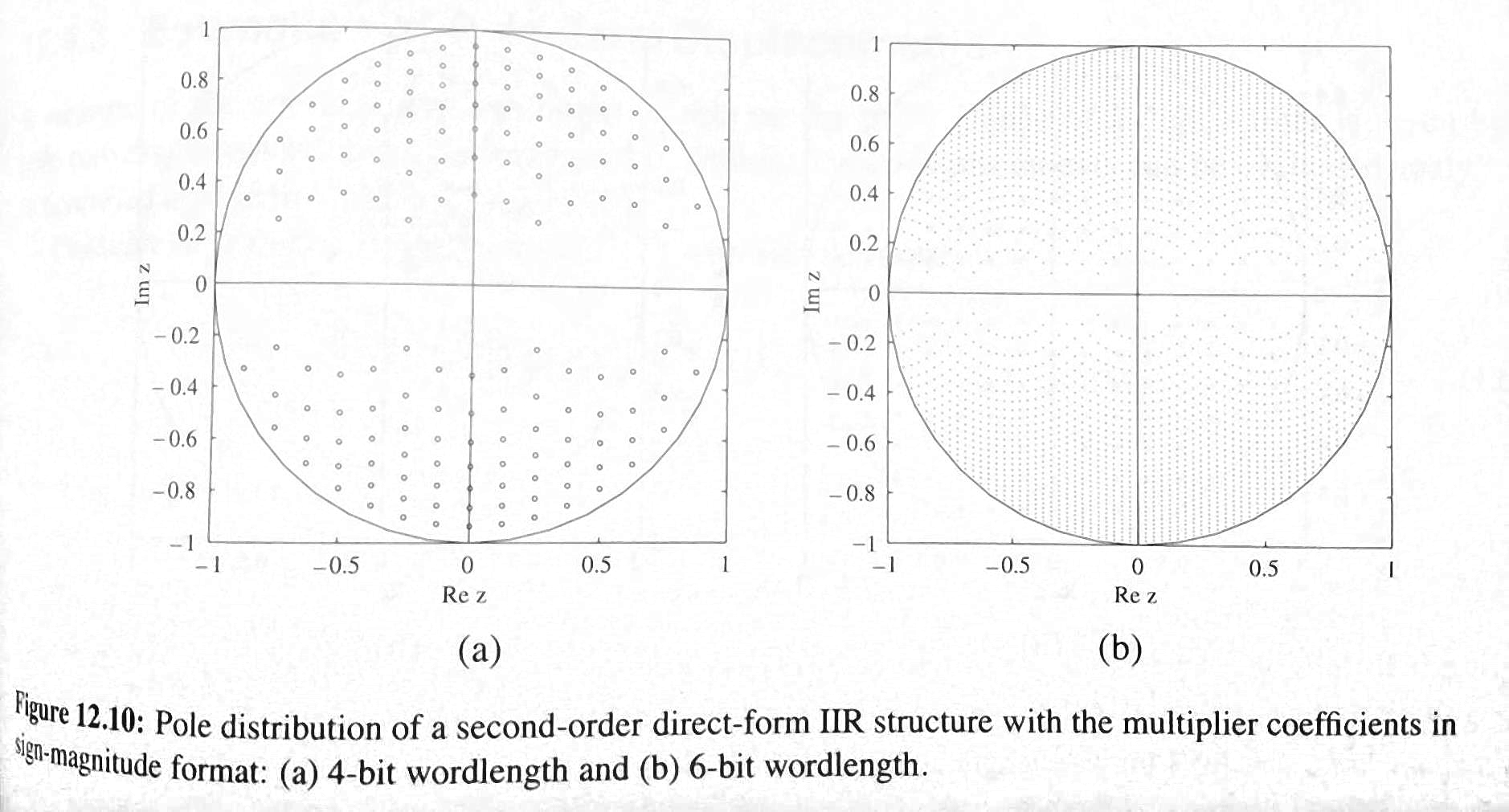
Limited-precision representation of coefficients limits realizable system parameters
Images from Digital Signal Processing with Student CD ROM 4th Edition by Sanjit Mitra
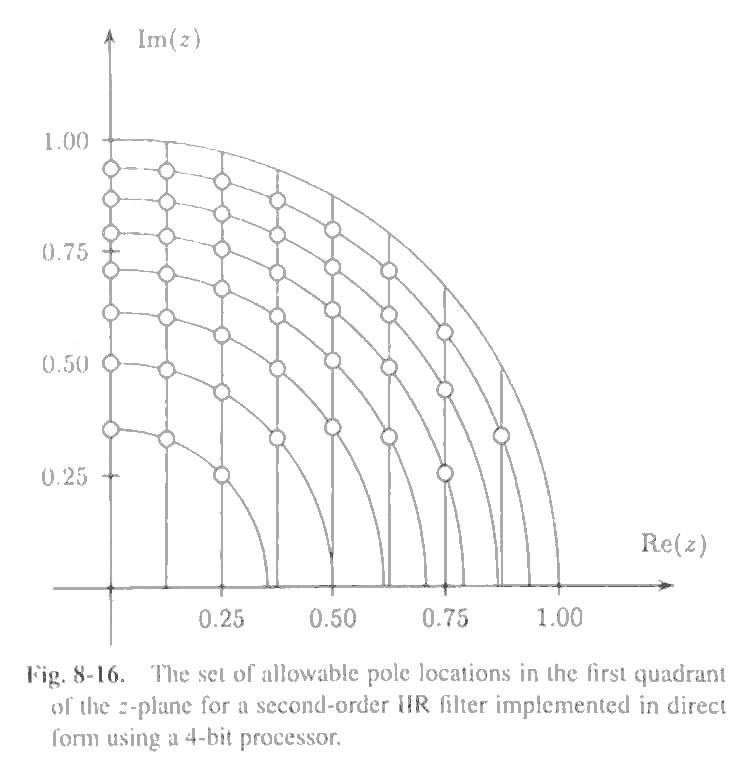
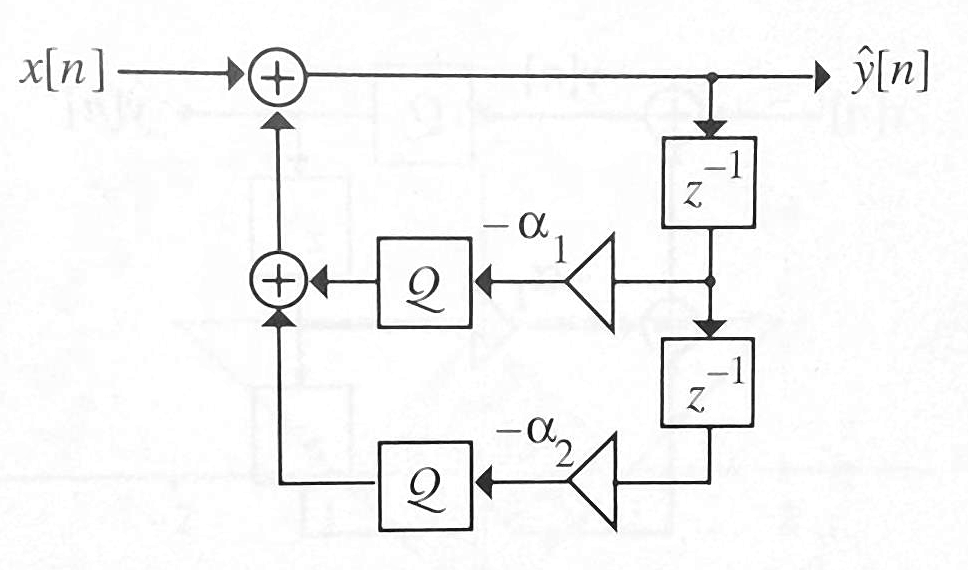
Direct-form II very poor for high-pass below pass filters requiring pole near the real axis

Manipulation of the order of operations can yield different possible system realizations Here is a equivalent system if infinite precision is used, but yields different results if parameters and calculations are of limited precision
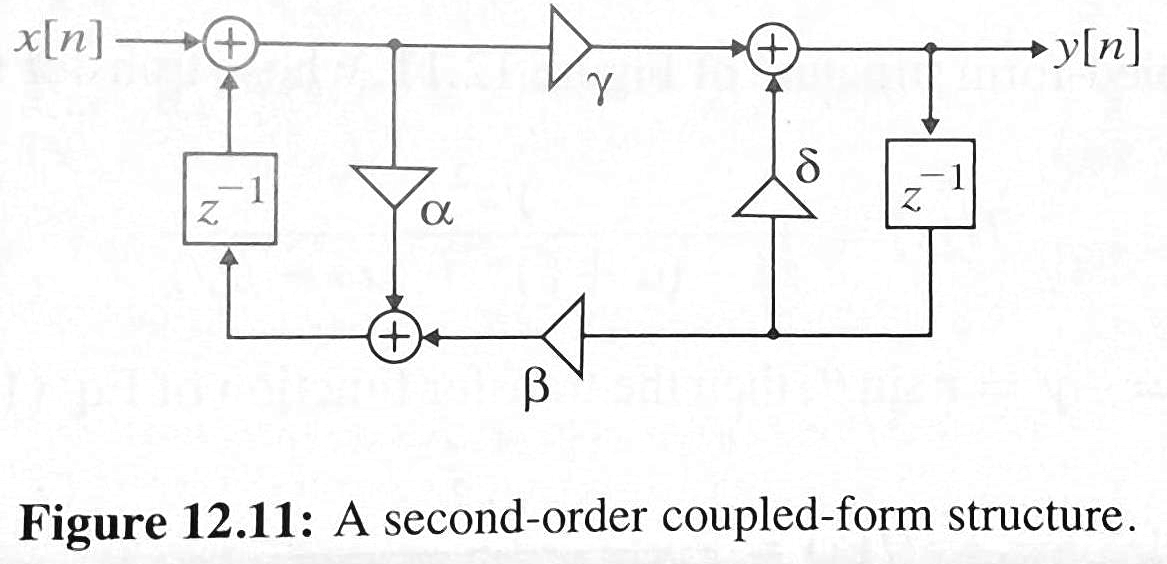
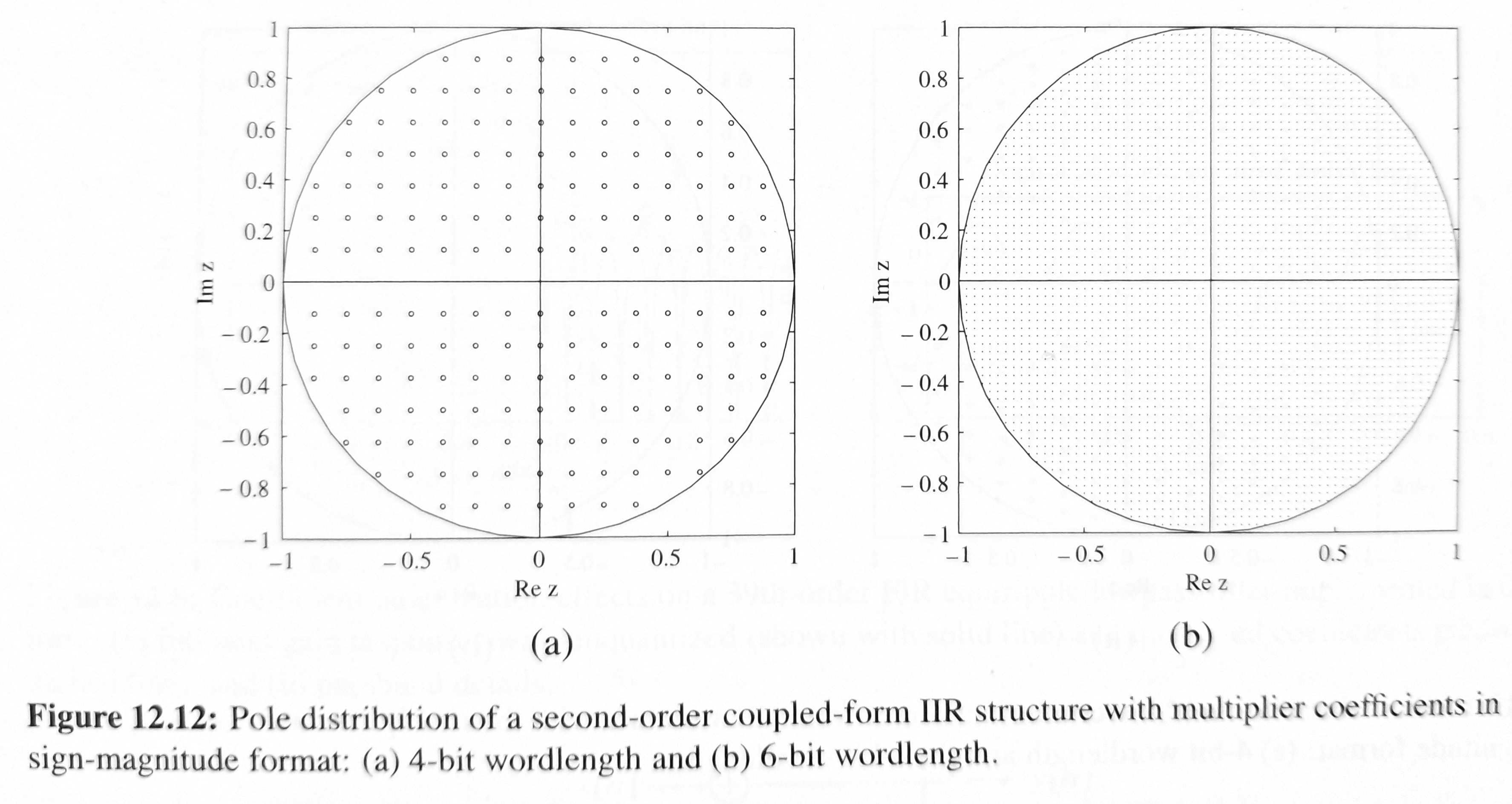
Eliminating Overflow or Saturation
- Overflow may occur at the output and at many points within a system
- If overflow is possible at the output of the accumulators and cannot be stored into the delay storage registers
- A solution is to pre-downscale inputs or added downscales at internal within the system (e.g. divide x by a necessary factor), but at the cost of effective precision

Saturation
- When choosing scales, range and precision are traded
- Detect overflow condition – override output to avoid LARGE roll-over error from modulus arithmetic
- If result exceeds 2N−2−1 replace with 2N−2−1
- If result exceeds −2N−2 replace with 2N−2
- 3 input MUX
- Balanced Range
- Using limits 2N−2−1 and −(2(N−1)) under some conditions may cause bias (non-zero average error) , might be better to limit to 2m−2−1 and −(2N−1−1)
Soft Max
- Choosing Smoother Limiting Functions will smooth the estimated wave by "compressing" past a soft limit. The saturation error is smoothed and high-frequency distortion is mitigated.
- A linearized approach can be implemented cheaply using a scale for signal components exceeding a softlimit (may involve scale by const or scale by power of two)
- Smoother sigmoidal functions mimicking analog circuits can be used as well
- In-Class Soft-Limited Sinusoidal Wave Shown
Quantization / Round-off Noise
When error is small compared to a signal, quantization error is model as noise, in fact it is nearly ideal to model the error as white noise when the error very small compared to the signal (high SNR)
- A computation stage can be modeled using an ideal calculation followed by additive error
- Limited-precision effects are modeled as quantization error and analyzed as if noise is inserted into the system at the quantization/round-off step
- Good SNR (signal to noise ratio) demands that the signal's actual range in an application be large compared to the round-off error
Limit Cycles
- "Limit Cycles" are a special case of quantization (limited precision) error
- IIR systems can exhibit "limit cycles," indefinite oscillatory responses from either round-off or overflow errors. This is possible from the feedback of the Limited-precision error, and repetitive rounding.
- Errors may "appear" to be constant outputs or +/- oscillations, even after the input becomes 0
- FIR filters (no feedback) do not exhibit this
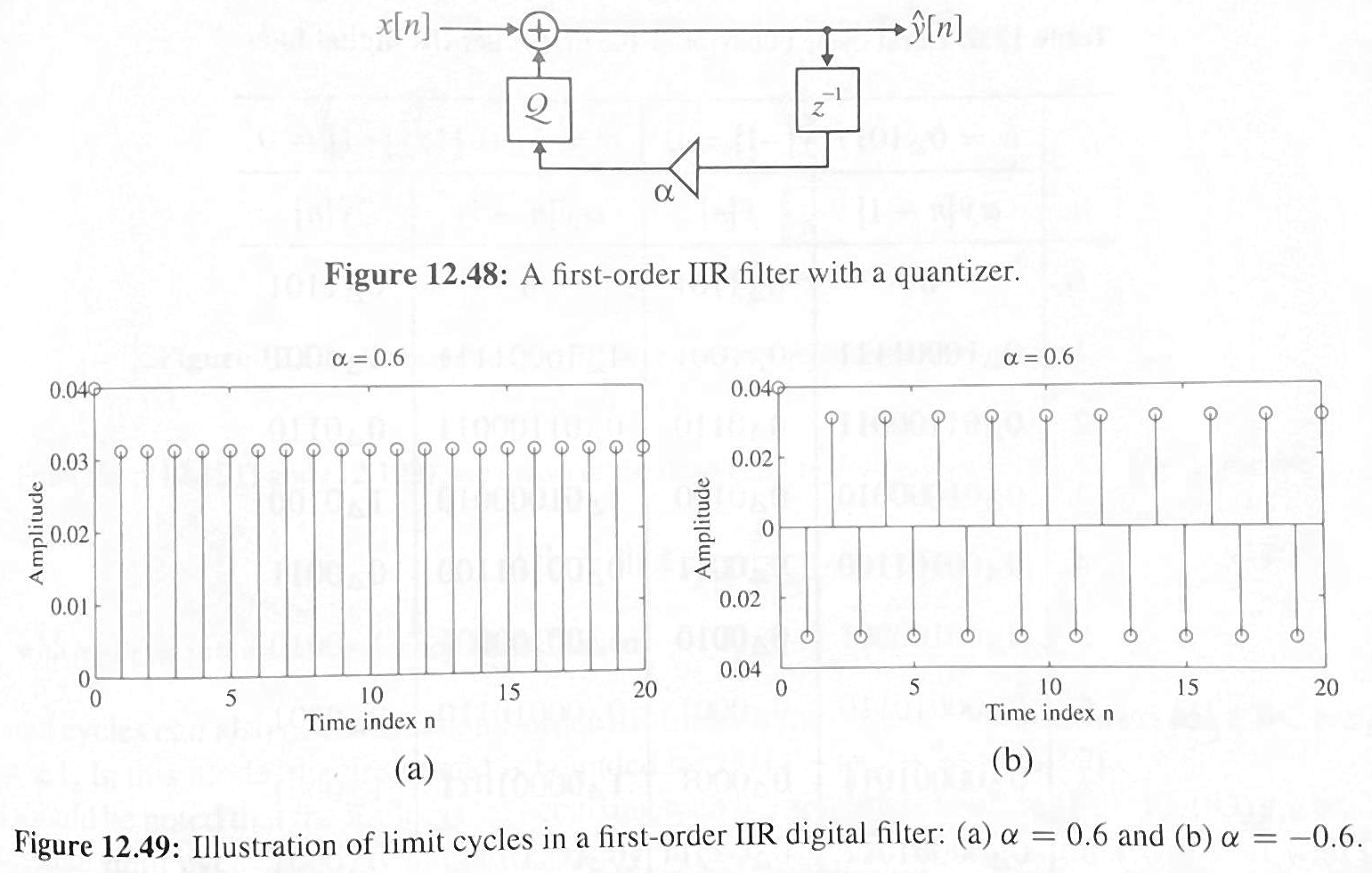
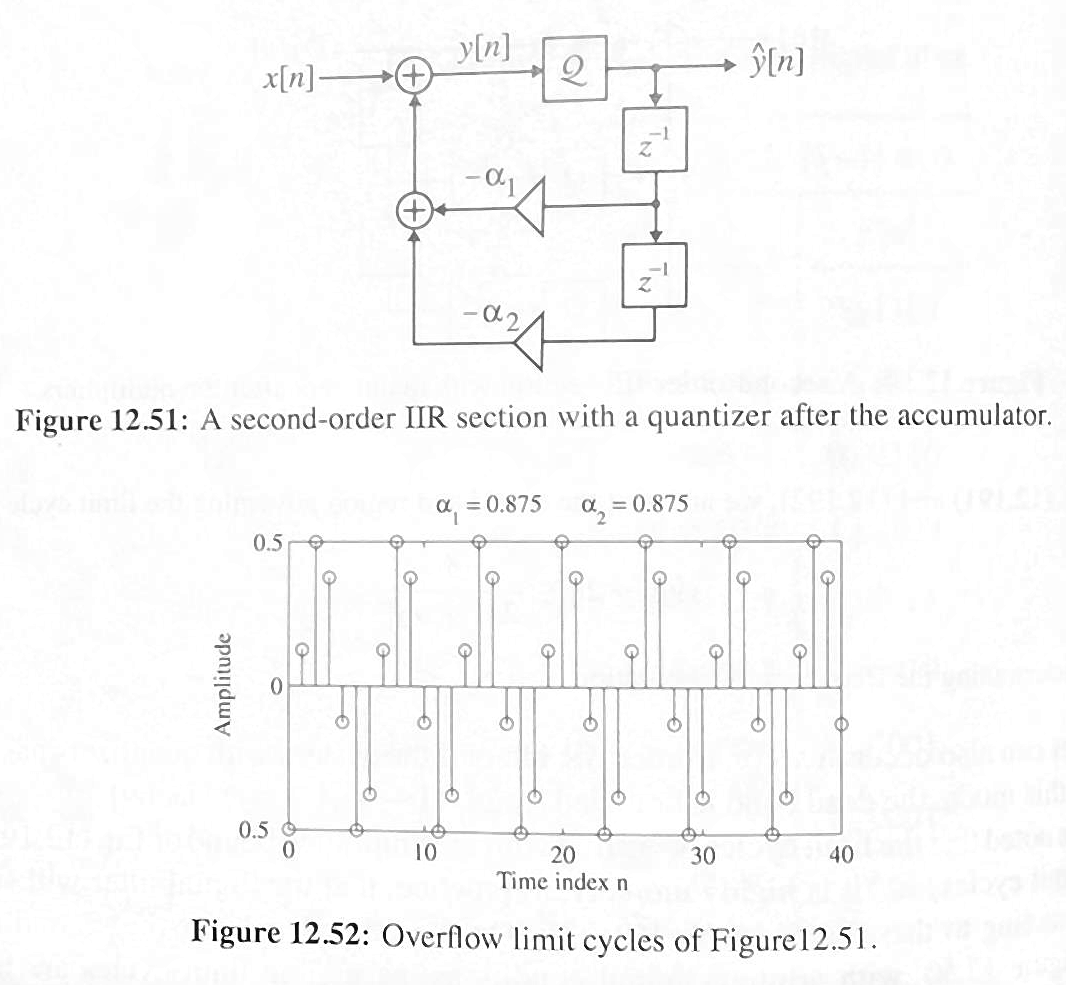
Techniques to avoid unwanted limited cycle behaviour usually involve increasing bit length of intermediate calculations, using increased bit length use feedback of error and feedback, introducing random quantization to mitigate perpetuating effects
Ref for Additional Examples:
Discrete-Time Signal Processing (3rd Edition) (Prentice-Hall Signal Processing Series) 3rd Edition by Alan V. Oppenheim (Author), Ronald W. Schafer
- Ex 6.15 steps through an example of this shows roundoff error where the output oscillates
- Ex 6.16 steps through an example of this shows overflow error- based oscillation which can be more sever
Addition and Overflow Detection
- Two's compliment addition of two numbers where the longest is N-bit can require up to N+1 bits to store a full result
- Two's compliment addition can only overflow if the signs of the operands are the same
- Overflow check: input sign bits are same and do not match result sign bit
Subtraction and Overflow Detection
- Two's compliment subtraction can only under/overflow if the signs of the operands are different, otherwise the magnitude of the result must be smaller than the maximum magnitude of the two operands.
- Overflow check: resulting sign bit does not match the first operand and the sign bits of the operands are different i.e. sign bit of the second operand and the result are the same and not equal to that of the first
Working with signed and unsigned reg and wire
Verilog 2001 provides signed reg and wire vectors
Casting to and from signed may be implicit or may be explicit by using
$unsigned()Ex:reg_s=$unsigned(reg_u);$signed()Ex:reg_u=$unsigned(reg_s);
Implicit or Explicit Casting is always a dumb conversion (same as C), they never change bits, just the interpretation of the bits (e.g. -1 is not round to 0 upon conversion to unsigned, it is just reinterpreted as the largest unsigned value) for subsequent operations by the compiler/synthesizer
- If a mix of signed and unsigned operands are provided to an operator, operands are first cast to be unsigned (like C)
Signed/Unsigned Casting may be followed by length adjustment.
Truncation and Extension
- Truncation and Extension may be implied by context in Verilog.
- Review of Truncation and Extension for Arithmetic Operators Discussion.
Truncation
- Assignment to a shorter type is always just bit truncation (no smart rounding such as unsigned(-1) → 0 )
Error Checking: - For unsigned, truncation is no problem as long as all the truncated bits are 0 (ex: 0000101 (5) can truncate up to 3 bits)
- For signed, truncation is no problem as long as all the bits truncated are the same AND they match the surviving msb (ex: 1111100 (-3) can truncate up to 4 bits)
Extension
- Assignment to a longer type is done with either zero or sign extension depending on the type:
- Unsigned types use zero extension
- Signed types use sign extension
Rules for expression bit lengths
- A self-determined expression is one in which the length of the result is determined by the length of the operands or in some cases the expression has a predetermined length for the result.
- Ex: as self-determined expression the result of addition has a length that is the maximum length of the two operands.
- Ex: a comparison is always a self-determined expression with a 1-bit result
- However, addition and other operation expressions may act as a context-determined expression in which the bit length is determined by the context of the expression that contains it, such as with an addition coupled with an assignment.
Addition
In this example we see that addition obeys modular arithmetic with a result u8y=0
ur8a = 128; ur8b = 128; ur8y= ur8a+ur8b;
In this example we see that the addition is an expression paired with an assignment, so the length of the assigned variable sets the context-determined expression operand length of the addition to take on the length of the largest operand, 9-bits. Using zero-extension in this case, the addition operands are each extended to 9-bits before addition.
ur8a = 128; ur8b = 128; ur9y= ur8a+ur8b; //9-bit addition
Self-Determined Expression and Self-Determined Operands
- Some operators always represent a self-determined expression, they have a well-defined bit-length that is independent of the context in which they are used and must be derived directly from the input operand(s) (the result may still be extended or truncated as needed). These may also force the operands to obey their self-determined expression bit length.
- The concatenation operator is one such example of a self-determined expression with a bit-length that is well-defined as the sum of length of its operands, and in turn its operands are forced to use their self-determined expression length.
- Single-operand : e.g.
{a}for which the result is the length ofa - Multiple operands: e.g.
{2'b00,b,a}for which the result length is 2+length(b)+length(a)
- Single-operand : e.g.
- The use of a single operand {} can force a self-determination for expressions like addition:
- In this next example, the self determined length of the addition is 8-bits which results in 0 for the summation. The 8-bit result from the concatenation operator is always unsigned and thus is zero extended.
The result is 'ur9y=256'
ur8a = 128; ur8b = 128; ur16y= {ur8a+ur8b}; //8 bit addition ur16z= ur8a+ur8b; //16 bit addition
- In this next example, the self determined length of the addition is 8-bits which results in 0 for the summation. The 8-bit result from the concatenation operator is always unsigned and thus is zero extended.
Rules for expression bit lengths from IEEE Standards Doc.
5.4.1 Rules for expression bit lengths
The rules governing the expression bit lengths have been formulated so that most practical situations have a natural solution.
The number of bits of an expression (known as the size of the expression) shall be determined by the operands involved in the expression and the context in which the expression is given.
A self-determined expression is one where the bit length of the expression is solely determined by the expression itself—for example, an expression representing a delay value.
A context-determined expression is one where the bit length of the expression is determined by the bit length of the expression and by the fact that it is part of another expression. For example, the bit size of the right-hand expression of an assignment depends on itself and the size of the left-hand side.
Table 5-22 shows how the form of an expression shall determine the bit lengths of the results of the expression. In Table 5-22, i, j, and k represent expressions of an operand, and L(i) represents the bit length of the operand represented by i.
Multiplication may be performed without losing any overflow bits by assigning the result to something wide enough to hold it.
Reference from IEEE Standards Doc.

Getting the IEEE Verilog Specification
At UMBC, goto http://ieeexplore.ieee.org/
Search for IEEE Std 1364-2005
You'll find
- IEEE Standard for Verilog Hardware Description Language IEEE Std 1364-2005 (Revision of IEEE Std 1364-2001)
- older standard 1995 standard and the SystemVerilog standard
Addition and Mixed Sign
Addition in the context with of assignment will cause extension of operands to the size of the result (the synthesizer may later remove useless hardware). However, the extension is performed according to the type of addition, which is determined by the operands. Therefore, signed extension is only performed if BOTH operands are signed regardless of the assignment.
module test(); reg signed [7:0] s; reg [7:0] u; reg signed [7:0] neg_two; reg [15:0] x1,x2; reg signed [15:0] y1,y2;
initial begin neg_two = -2; s = 1; u = 1; x1 = u + neg_two; x2 = s + neg_two; y1 = u + neg_two; y2 = s + neg_two; $display("%b",x1); $display("%b",x2); $display("%b",y1); $display("%b",y2); end endmodule
Result:
0000000011111111
1111111111111111
0000000011111111
1111111111111111
Pitfall Example
. . . reg [3:0] bottleStock = 10; //**unsigned** always @ (posedige clk, negedge rst_) if (rst_==0) bottleStock<=10; else if (bottleStock >= 0) //always TRUE!!! bottleStock <= bottleStock-1;
Pitfall Example
. . . input wire [2:0] remove; signed reg [3:0] remainingStock = 10; //**signed** always @ (posedige clk, negedge rst_) if (rst_==0) remainingStock<=10; else if ((remainingStock-remove) >= 0) //always TRUE!!! remainingStock <= remainingStock-remove;
Scaling by Powers of Two
- Multiplying by a positive integer power of two may be performed with the logical left-shift shift operator
- Multiplying by 2^k is left shift by k:
a<<k- Typically synthesizers require k to be a constant;
- k bits on left are discarded
- Detecting Overflow: no overflow if all discarded bits are the same and the new msb matches the truncated bits
- Logical Shifting is usually inexpensive – just “rewiring”.
Multiplication
In general to hold the result you need M+N bits where M and N are the length of the operands
wire [N-1:0] a; wire [M-1:0] b; wire [M+N-1:0] y; y=a*b;
The multiplication in the context with the assignment will cause extension of operands to the size of the result (the synthesizer may later remove useless hardware). However, the extension type is performed according to the type of input operands (signed extension is only performed if BOTH operands are signed)
Multiplication
- Multiplication by two variables can be expensive, with a size on the order of MxN (full 1-bit adders and
ANDgates as 1-bit mult) - Delay is proportional to M+N
1011 (M bits) x 10010 (Nbits):
- FPGA may have banks of “hard” multipliers (e.g. 8x8 multipliers, sometime in what is called DSP slices) so as to avoid using large portions of the programmable fabric. Ex. 8-bit multipliers can be used for 16-bit mult, mathematically shown: Y = {AH,AL} x {BH,BL} = AHBH<<16+AHBL<<8+ALBH<<8+ALBL. The synthesizer will recognize the size of the multiplication block construct the mapping to available multipliers for you.
Multiplication Overflow Check Ideas:
- can compute full result and check truncation
- can can partial products and check for overflow that word occur in sifting partial products and after additions
- can compute full result then divide and compare to input
Multiplication by Constants
Multiplication by constants with only few non-zero bits can be inexpensive:
u∗24=u∗(16+8)=u<<4+u<<3
This concept is important for computer engineer to have in their tool belt.
Using example from previous slide: if the second operand is a constant, the synthesizer reduces the multiplication to shift and one adder:
Rounded Integer Division
- Rounded-result division of integers A,B may be accomplished by effectively adding a bias matching the sign of the result, that is adding an offset(bias) to A that is half the magnitude of the divisor B (integer division half) and matches the sign of the numerator
|round(float(A)/float(B))| = (|A|+|B/2|)/|B| - Why: Because integer division is round towards 0, but if ∣A%B∣ is at least half of ∣B∣ then we need to round away from 0, which can accomplished by effectively adding 0.5 to the magnitude of the result before rounding
A+(|B|*sign(A))/2wheresign(A)is 1 or -1 according to the sign of A
- Exercise: Try to make code to divide a integer (signed), S, by 256 with a rounded result
result = (S>=0) ? ((S+128)/256) : ((S-128)/256); - Exercise: Try to make code to divide a integer (signed), S, by 5 with a rounded result
result = (S>=0) ? ((S+2)/5) : ((S-1)/5); - A synthesizer may only support division by powers of two and possibly only constants
Rounded Division (w/ power of 2 den. example)
- float to int conversion is floating-point
fix()operator (subtract fractional part) with type conversion discarding fractional part - int division x/y is same as floating point division followed by int conversion
- Does not achieve rounding result, requires a bias: (x+sign(x)×y/2)/y
Rounded Division (non-power-of-2 denominator)

Properly Mimic Integer-Divide by Powers of Two
- Divide x by 2k is almost the same as an arithmetic right shift
- discard k bits on the right and replicate sign bit k times on the left. Must use the arithmetic shift to perform sign extension;
x>>>k;same as{k{x[msbindex]},x[msbindex:k]} - However, “integer division” is defined by truncation of the fractional bits of the result, also known as “round towards zero” To mimic this behavior more is needed:
This is
- For a positive x corresponds to
floor(x/n)ex: 5/2 = 2 - For a negative x it corresponds to
ciel(x/n)ex: -5/2= -2 - If x is positive you can just use logical shifting:
x>>k; - If x is negative, we want ciel(x/n) which may be computed by applying a bias that 1 LSB less than the divisor … this is just enough bias that with any fractional result the value becomes ''bigger'' than the next ''bigger'' negative integer:
floor((x-(2k-1))/(2k))In verilog:(x -((1<<k)-1)) >>> k
Arbitrary Precision Arithmetic for Longer numbers
- Embedded systems can implement larger word-length operations, which is a reasonable alternative to using a more complex processor if needs are not at timing-critical points in time.
- For 16 bit calculations, an 8-bit architecture may support double-register arithmetic (e.g. use two registers to hold output of a 8X8 multiplication)
- For even longer numbers results can be calculated a piece at a time and overflow bits (add/sum) or overflow registers (multiply) can be used to compute larger results. The built-in C variable types are usually automatically handled by the compiler. If even longer types are needed, find an arbitrary precision arithmetic software library.
Fixed-point arithmetic
Floating Point Math and Fixed-Point Math
- If no floating point unit (FPU) is available, you can find a floating point software library. This will likely be slow.
- Another option is fixed-point math. You can write or use a library or just do it as needed inline….
Fixed-point arithmetic
Want to use integer operations to represent adding 0011.1110 and 0001.1000
Solution:
- Store
0011.1110as00111110 - Store
0001.1000as00011000 - Add
00011000+00111110=01010110 - Interpret
01010110as0101.0110
Use QM.N format: M+N bits, with M bits as whole part and N bits as fractional part
Fixed-point arithmetic
Up to you to determine number of bits to use for whole and fraction parts depending on range and precision needed. This determines the scale factors required to convert the faction to a whole number
1101.0000 * 16 = 11010000 S=16, Q4.4
01.011000 * 64 = 01011000 S=64, Q2.6
Addition with scale S:
A+Bcomputed asA*S+B*S=C*S- Divide result by S to obtain answer C
- using a power of two for S is efficient, though not required
Subtraction with scale S:
A-Bcomputed asA*S-B*S=C*S- Divide result by S to obtain answer C
Multiplication with scale S
A*Bcomputed as(A*S)*(B*S)=C*S2D- Divide result by S2
- to obtain answer C divide result by S to obtain scaled answer C*S which you can use in further scale S calculations
- Unfortunately, the intermediate result
C*S*Srequired more storage than the scaled resultC*S
Division with scale S:
A/Bcould be computed as(A*S)/(B*S)=C- Scales cancel. Which is fine if you only wanted an integer answer
- Would need to multi by S to obtain scaled result C*S for further math
- …but this is less accurate since the lower bits have already been lost
- Better to prescale one of the operands
((A*S)*S)/(B*S)=C*S - Unfortunately, the intermediate term
((A*S)*S)required more storage and a larger computation
Additional Operations
Equality Comparison
wire signed [7:0] x,y; wire flagEq; flagEq = (x==y); implements eight xnor2 followed by and8;
Magnitude Comparator
- Can also use subtraction and check for zero and sign bits
- Comparison Chain (just x>y)
representative circuit:
- 4-Bit "Full" Magnitude Comparator Sharing Intermediate Terms
Ref: http://www.ti.com/lit/ds/symlink/sn74ls85.pdf
